Dr. Ron Licht 11 - 1 www.structuredindependentlearning.com
Physics 20 Lesson 11
Vector Addition – Components
In Lesson 10 we learned how to add vectors which were perpendicular to one another
using vector diagrams, Pythagorean theory, and the tangent function. What about
adding vectors which are not at right angles or collinear with one another? In this
lesson, we will learn about the component method.
I. Component method
(It is strongly recommended that you read pages 83 to 90 in Pearson for a good
discussion on vector addition using components.)
As we learned in Lesson 10, when several vectors are being added together, the north-
south vectors may be added together to form one north-south vector, while the east-
west vectors can be added to form
one east-west vector. The single
north-south vector is then added
to the single east-west vector to
form a triangle with the resultant
vector as the hypotenuse. This
process works fine if the vectors
being added together are all east-
west or north-south vectors.
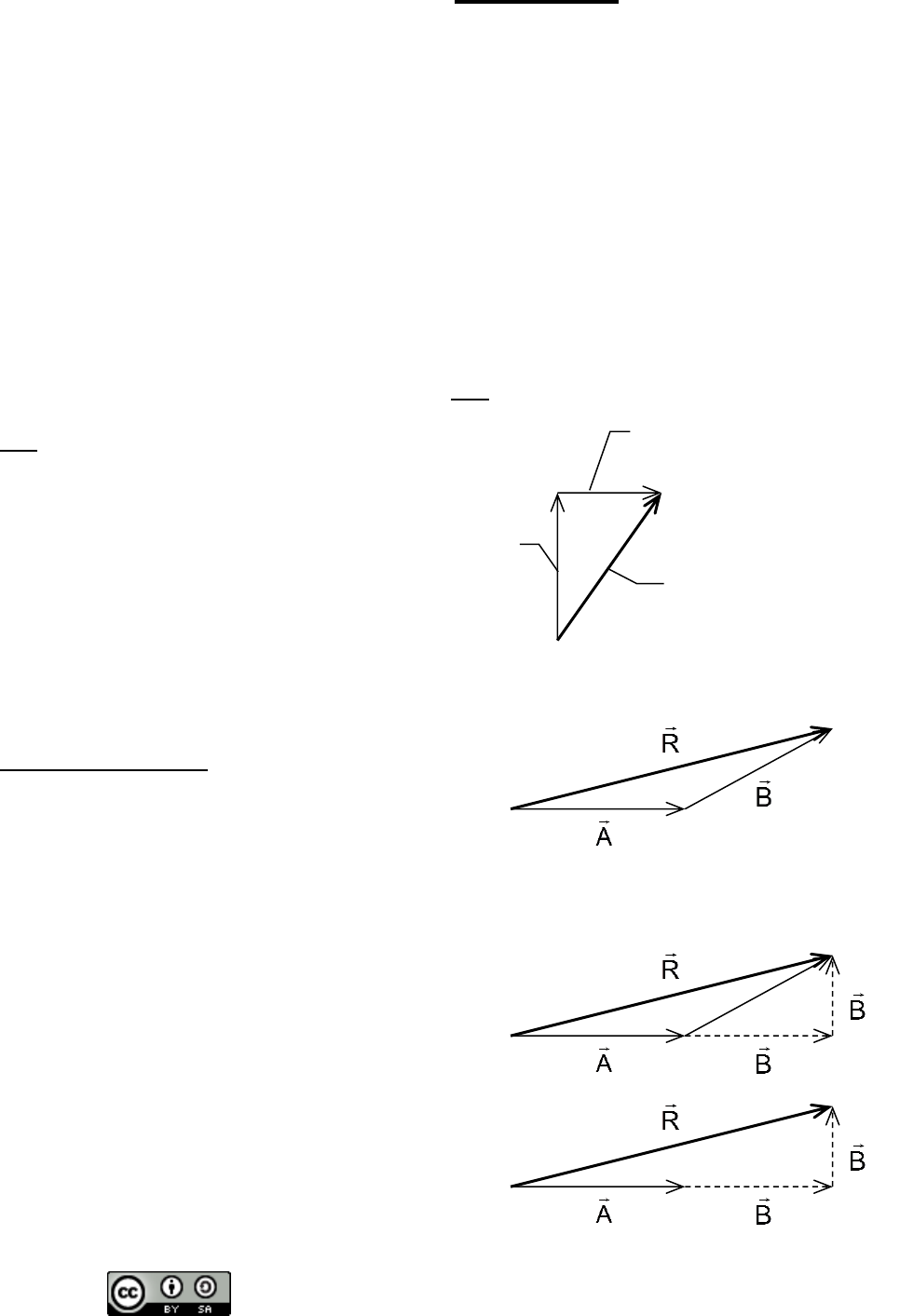
However, what if one or more of the vectors is at an angle from north-south or east-
west? For example, consider vectors
A
and
B
being added together to form the
resultant vector
R
. The basic idea of the
component method of vector addition is to first
convert all the vectors being added into their
north-south and east-west components. Then the
north-south components and east-west
components are added together to form one
north-south vector and one east-west vector. When these are added together they form
a single resultant vector.
In our current example, vector
A
east vector, therefore nothing is done to it.
Vector
B
is converted into its components
B
x
and
B
y.
In effect, the component method
eliminates vectors like vector
B
components. The result is a new triangle where
A
+
B
x
forms one side and
B
y
forms the other
side. Now we can use the Pythagorean theorem
and the tangent function to find the magnitude
and direction of vector
R
.
east-west
north-south
resultant
x
y
x
y

Dr. Ron Licht 11 - 2 www.structuredindependentlearning.com
Before continuing, we must learn how to calculate the components of vectors. Using
vector
A
= 50 m [30° N of E] as an example
This vector can be resolved into an east (x) component and a north (y) component. By
treating the vector as the hypotenuse of a right triangle, we can draw in the components
of the vector as the adjacent and opposite sides of the right triangle. Notice when this is
drawn properly the components have arrows to indicate their directions.
For this particular vector,
A
x
is the adjacent side and it can be calculated using the
cosine function:
x
x
x
adj
cos30
hyp
A
cos30
50
A 50cos30
A 43.3m east
The north component (
A
y
) is the opposite side and can be found using the sine function:
y
y
A 50sin30
A 25m north
Example 1
Calculate the east-west and north-south components for the acceleration 25.0 m/s
2
[215
o
].
Correctly draw the vector and draw the components of the vector. Then calculate
using the appropriate trig. functions.
30
o
50 m
North component
y
East component
x
30
o
50 m
cah
x
= 20.5 m/s
2
[W]
soh
y
= 25.0 sin 35
y
= 14.3 m/s
2
[S]
x
y
25 m/s
2
35
o
215
o

Dr. Ron Licht 11 - 3 www.structuredindependentlearning.com
Example 2
A man walks 40 m [30° N of E], then 70 m [60° S of E], and finally 20 m [45° N of W].
What is the displacement of the man?
1. Our first task is to find the components of any vector that is not straight north,
south, east or west. In this example, all of the vectors need to be reduced to their
components.
2. Since we now have a problem that has straight North, South, East and West
vectors, we follow the same procedure as outlined in Lesson 10.
(North - South)
20 m [N] + 60.62 m [S] + 14.14 m [N] = 26.48 m south
(East - West)
34.64 m [E] + 35 m [E] + 14.14 m [W] = 55.5 m east
3. Drawing a vector diagram we can calculate the resulting displacement.
d
= 61.5 m [64.5
o
E of S]
26.48 m
55.5 m
x
y
40 m
30
o
x
= 40 cos 30
x
= 34.64 m [E]
y
= 40 sin 30
y
= 20 m [N]
y
x
60
o
70 m
x
= 70 cos 60
x
= 35 m [E]
y
= 70 sin 60
y
= 60.62 m [S]
x
y
45
o
20 m
x
= 20 cos 45
x
= 14.14 m [W]
y
= 20 sin 45
y
= 14.14 m [N]
1
1
o
opp
tan
adj
55.5
tan
26.48
64.5 Eof S
22
d 55.5 26.48
d 61.5m

Dr. Ron Licht 11 - 4 www.structuredindependentlearning.com
II. Practice Problems
1. A turtle walks 60 m [210
o
], then 50 m [45
o
W of N] and then 60 m [0
o
]. What was
the turtle’s final displacement? (27.8 m [11
o
N of W])

Dr. Ron Licht 11 - 5 www.structuredindependentlearning.com
III. Hand-in Assignment
1. For each of the following vectors calculate the east-west and north-south
components.
A. 25 m/s [40
o
E of N] (16.1 m/s east, 19.2 m/s north)
B. 16 m/s
2
[20
o
S of W] (15.0 m/s
2
west, 5.5 m/s
2
south)
C. 45 km [15
o
N of E] (43.5 km east, 11.6 km north)
2. A woman walks 440 m [50
o
S of W] and then 580 m [60
o
N of E]. The entire trip
required 15 minutes
A. What was the total distance travelled? (1020 m)
B. What was the displacement of the woman? (165.4 m [2.5
o
E of N])
C. What was the average speed of the woman in m/min? (68 m/min)
3. A man walks 440 m [50
o
W of S] and then 580 m [60
o
E of N]. The entire trip
required 15 minutes
A. What was the total distance travelled? (1020 m)
B. What was the displacement of the man? (165.4 m [2.5
o
])
C. What was the average speed of the man in m/min? (68 m/min)
4. A boy runs at 5.0 m/s [30
o
S of W] for 2.5 minutes and then he turns and runs at
3.0 m/s [40
o
S of E] for 4.5 minutes.
A. What was his average speed? (3.7 m/s)
B. What was his displacement? (896 m [1.9
o
W of S])
5. A man walks 600 m [47
o
N of E], then 500 m [38
o
W of N], then 300 m [29
o
S of W],
and finally 400 m [13
o
E of S]. Find his resultant displacement. (306 m [13
o
W of N])
6. A slightly disoriented homing pigeon flies the following course at a constant speed
of 15 m/s:
(i) 800 m [37
o
E of N]
(ii) 300 m due west, and
(iii) 400 m [37
o
S of E]
A crow flies in a straight line (as the crow flies) between the starting and finishing
points. At what speed must the crow fly, if the birds leave and arrive together? (6.4
m/s)
7. An airplane is climbing at an angle of 15
o
to the horizontal with the sun directly
overhead. The shadow of the airplane is observed to be moving across the
ground at 200 km/h. (a) What is the actual airspeed of the plane? (b) How long
does it take for the plane to increase its altitude by 1000 m? (207 km/h, 1.1 min)
For extra practice, do the practice problems on page 88 of Pearson.
