Department of Civil Engineering B.TECH

Department of Civil Engineering

B.TECH – 5

TH

SEM

Lecture Notes on

STRUCTURAL DESIGN

BCE301

Disclaimer

This document does not claim any originality and cannot be used as a substitute for

prescribed textbooks. The information presented here is merely a collection by the committee

members for their respective teaching assignments. We would like to acknowledge various

sources like freely available materials from internet particularly NPTEL course material from

which the lecture note was prepared. The ownership of the information lies with the

respective authors or institutions. Further, this document is not intended to be used for

commercial purpose and the committee members are not accountable for any issues, legal or

otherwise, arising out of use of this document. The committee members make no

representations or warranties with respect to the accuracy or completeness of the contents of

this document and specifically disclaim any implied warranties of merchantability or fitness

for a particular purpose.

Syllabus

Module-I

Properties of concrete and reinforcing steel, Philosophy, concept and methods of reinforced

concrete design, Introduction to limit state method: Limit state of collapse and limit state of

serviceability. Application of Limit state method to rectangular beams for flexure, shear,

bond and torsion.

Module-II

Design of doubly reinforced beams. Design of T-and L-beams. Design of one way and two

way slabs, Design of staircases.

Module-III

Design of short and long columns with axial and eccentric loading, design of isolated column

footing.

Module-IV

Design principle of masonry structures: Brick and stone masonry. Design of masonry short

and long walls, columns and retaining walls.

Reference Books:

1. Limit state design of reinforced concrete by P.C. Verghese, PHI

2. Reinforced concrete: Limit state by A.K. Jain

3. Reinforced concrete by B.C. Punmia, A.K. Jain and A.K. Jain

4. SP-16 and SP-32.

MODULE-1

Introduction

Reinforced concrete, as a composite material, has occupied a special place in the modern

construction of different types of structures due to its several advantages. Due to its flexibility

in form and superiority in performance, it has replaced, to a large extent, the earlier materials

like stone, timber and steel. Further, architect's scope and imaginations have widened to a

great extent due to its mouldability and monolithicity. Thus, it has helped the architects and

engineers to build several attractive shell forms and other curved structures. However, its role

in several straight line structural forms like multistoried frames, bridges, foundations etc. is

enormous.

Concrete

Concrete is a product obtained artificially by hardening of the mixture of cement, sand, gravel

and water in predetermined proportions.

Depending on the quality and proportions of the ingredients used in the mix the properties of

concrete vary almost as widely as different kinds of stones.

Concrete has enough strength in compression, but has little strength in tension. Due to this,

concrete is weak in bending, shear and torsion. Hence the use of plain concrete is limited

applications where great compressive strength and weight are the principal requirements and

where tensile stresses are either totally absent or are extremely low.

Properties of Concrete

The important properties of concrete, which govern the design of concrete mix are as follows

(i) Weight

The unit weights of plain concrete and reinforced concrete made with sand, gravel of crushed

natural stone aggregate may be taken as 24 KN/m

3

and 25 KN/m

3

respectively.

(ii) Compressive Strength

With given properties of aggregate the compressive strength of concrete depends primarily on

age, cement content and the water cement ratio are given Table 2 of IS 456:2000.

Characteristic strength are based on the strength at 28 days. The strength at 7 days is about

two-thirds of that at 28 days with ordinary portland cement and generally good indicator of

strength likely to be obtained.

(iii) Increase in strength with age

There is normally gain of strength beyond 28 days. The quantum of increase depends upon

the grade and type of cement curing and environmental conditions etc.

(iv) Tensile strength of concrete

The flexure and split tensile strengths of various concrete are given in IS 516:1959 and IS

5816:1970 respectively when the designer wishes to use an estimate of the tensile strength

from compressive strength, the following formula can be used

Flexural strength, f

cr

 

ck

N/mm

2

(v) Elastic Deformation

The modulus of elasticity is primarily influenced by the elastic properties of the aggregate

and to lesser extent on the conditions of curing and age of the concrete, the mix proportions

and the type of cement. The modulus of elasticity is normally related to the compressive

characteristic strength of concrete

E

c

 

ck

N/mm

2

Where Ec= the short-term static modulus of elasticity in N/mm

2

f

ck

=characteristic cube strength of concrete in N/mm

2

(vi) Shrinkage of concrete

Shrinkage is the time dependent deformation, generally compressive in nature. The constituents

of concrete, size of the member and environmental conditions are the factors on which the total

shrinkage of concrete depends. However, the total shrinkage of concrete is most influenced by the

total amount of water present in the concrete at the time of mixing for a given humidity and

temperature. The cement content, however, influences the total shrinkage of concrete to a lesser

extent. The approximate value of the total shrinkage strain for design is taken as 0.0003 in the

absence of test data (cl. 6.2.4.1).

(vii) Creep of concrete

Figure1.1: Stress-strain curve of concrete

Creep is another time dependent deformation of concrete by which it continues to deform,

usually under compressive stress. The creep strains recover partly when the stresses are

released. Figure 1.2.2 shows the creep recovery in two parts. The elastic recovery is

immediate and the creep recovery is slow in nature.

Thus, the long term deflection will be added to the short term deflection to get the total

deflection of the structure. Accordingly, the long term modulus E

ce

or the effective modulus

of concrete will be needed to include the effect of creep due to permanent loads. The

relationship between E

ce

and E

c

is obtained as follows:

/

c c c

fE





Where,

c



=short term strain at the age of loading at a stress value of f

c

-efficient =

cr

c



cr



=ultimate creep strain



th

, 28

th

and 365

th

day of loading are 2.2, 1.6 and 1.1 respectively.

Then the total strain=

c

c cr

ce

f

E





Where, E

ce

= effective modulus of concrete.

From the above Equation, we have

1

c c c

ce

c cr c cr

fE

E



    



  

The effective modulus of E

ce

of concrete is used only in the calculation of creep deflection.

It is s

may also be noted that the ultimate creep strain

cr



does not include short term strain

c



. The

creep of concrete is influenced by

 Properties of concrete

 Water/cement ratio

 Humidity and temperature of curing

 Humidity during the period of use

 Age of concrete at first loading

 Magnitude of stress and its duration

 Surface-volume ratio of the member

(f) Thermal expansion of concrete

The knowledge of thermal expansion of concrete is very important as it is prepared and

remains in service at a wide range of temperature in different countries having very hot or

cold climates. Moreover, concrete will be having its effect of high temperature during fire.

The coefficient of thermal expansion depends on the nature of cement, aggregate, cement

content, relative humidity and size of the section. IS 456 stipulates (cl. 6.2.6) the values of

coefficient of thermal expansion for concrete /

o

C for different types of aggregate.

Workability and Durability of Concrete

Workability and durability of concrete are important properties to be considered. The

relevant issues are discussed in the following:

The workability of a concrete mix gives a measure of the ease with which fresh concrete can

be placed and compacted. The concrete should flow readily into the form and go around and

cover the reinforcement, the mix should retain its consistency and the aggregates should not

segregate. A mix with high workability is needed where sections are thin and/or

reinforcement is complicated and congested. The main factor affecting workability is the

water content of the mix. Admixtures will increase workability but may reduce strength. The

size of aggregate, its grading and shape, the ratio of coarse to fine aggregate and the

aggregate-to-cement ratio also affect workability to some degree.

Measurement of workability

(a) Slump test

The fresh concrete is tamped into a standard cone which is lifted off after filling and the

slump is measured. The slump is 2550 mm for low workability, 50100 mm for medium

workability and 100175 mm for high workability. Normal reinforced concrete requires fresh

concrete of medium workability. The slump test is the usual workability test specified.

(b) Compacting factor test

The degree of compaction achieved by a standard amount of work is measured. The

apparatus consists of two conical hoppers placed over one another and over a cylinder. The

upper hopper is filled with fresh concrete which is then dropped into the second hopper and

into the cylinder which is struck off flush. The compacting factor is the ratio of the weight of

concrete in the cylinder to the weight of an equal volume of fully compacted concrete. The

compacting factor for concrete of medium workability is about 0.9.

Durability of concrete

A durable concrete performs satisfactorily in the working environment during its anticipated

exposure conditions during service. The durable concrete should have low permeability with

adequate cement content, sufficient low free water/cement ratio and ensured complete

compaction of concrete by adequate curing. For more information, please refer to cl. 8 of IS 456.

Design mix and nominal mix concrete

In design mix, the proportions of cement, aggregates (sand and gravel), water and

mineral admixtures, if any, are actually designed, while in nominal mix, the proportions are

nominally adopted. The design mix concrete is preferred to the nominal mix as the former

results in the grade of concrete having the specified workability and characteristic strength

(vide cl. 9 of IS 456).

Batching

Mass and volume are the two types of batching for measuring cement, sand, coarse aggregates,

admixtures and water. Coarse aggregates may be gravel, grade stone chips or other man made

aggregates. The quantities of cement, sand, coarse aggregates and solid admixtures shall be

measured by mass. Liquid admixtures and water are measured either by volume or by mass (cl.

10 of IS 456).

Properties of reinforcing steel

Steel reinforcement used in reinforced concrete may be of the following types

(a) 1. Mild steel bars conforming to IS 432 (part-I)

2. Hot rolled mild steel conforming to IS 1139

(b) 1. Medium tensile steel conforming to IS 432 (part-I)

2. Hot rolled medium tensile steel.

(c) 1. Hot rolled High Yield Strength Deformed (HYSD) steel conforming to IS 1139.

2. Cold-worked steel HYSD bars steel conforming to IS 1786.

(d) 1. Hard drawn steel wire fabric conforming to IS 1566.

2. Rolled steel made from structural steel conforming to Is 226.

1. the most important characteristic of a reinforcing bar is its stress strain curve and the

important property yield stress or 0.2% proof stress, as the case may be.

2. The modules of elasticity E for these steel is 2x10

5

N/mn

2

.

3. Mild steel bars have yield strength of 250 N/mm

2

and hence it is known as Fe 250.

4. HYSD bars may be hot rolled high yield strength bars or cold rooked steel high strength

deformed bars. The latter are also known as cold twisted deformed bars or Tor steel and are

available in different grades

i) Fe 415 ii) 500 iii) Fe 550 having 0.2% proof stress as 415N/mm

2

, 500N/mm

2

and 550

N/mm

2

5. The reinforcing bars should have sufficient % of elongation.

6. Its coefficients of thermal expansion should be more or less equal to the cement concrete.

Stress-strain curves for reinforcement

Figure1.2: Stress-strain curve for Mild steel (idealised) (Fe 250) with definite yield point

Figure1.3: Stress-strain curve for cold worked deform bar

Figures 1.2 and 1.3 show the representative stress-strain curves for steel having definite yield

point and not having definite yield point, respectively. The characteristic yield strength f

y

of

steel is assumed as the minimum yield stress or 0.2 per cent of proof stress for steel having no

definite yield point. The modulus of elasticity of steel is taken to be 200000 N/mm

2

.

For mild steel, the stress is proportional to the strain up to the yield point. Thereafter, post

yield strain increases faster while the stress is assumed to remain at constant value of f

y

.

For cold-worked bars (Fig. 1.3), the stress is proportional to the strain up to a stress of 0.8 f

y

.

Thereafter, the inelastic curve is defined as given below:

Stress

Inelastic strain

0.80 f

y

Nil

0.85 fy

0.0001

0.90 fy

0.0003

0.95 fy

0.0007

0.975 fy

0.0010

1.00 fy

0.0020

Linear interpolation is to be done for intermediate values. The two grades of cold-worked

bars used as steel reinforcement are Fe 415 and Fe 500 with the values of fy as 415 N/mm2

and 500 N/mm2, respectively.

Method of RCC design

A reinforced concrete structure should be designed to satisfy the following criteria-

i) Adequate safety, in items stiffness and durability

iii) Reasonable economy.

The following design methods are used for the design of RCC Structures.

a) The working stress method (WSM)

b) The ultimate load method (ULM)

c) The limit state method (LSM)

Working Stress Method (WSM)

This method is based on linear elastic theory or the classical elastic theory. This method

ensured adequate safety by suitably restricting the stress in the materials (i.e. concrete and

steel) induced by the expected working leads on the structures. The assumption of linear

elastic behaviour considered justifiable since the specified permissible stresses are kept well

below the ultimate strength of the material. The ratio of yield stress of the steel reinforcement

or the cube strength of the concrete to the corresponding permissible or working stress is

usually called factor of safety.

The WSM uses a factor of safety of about 3 with respect to the cube strength of concrete and

a factor of safety of about 1.8 with respect to the yield strength of steel.

Ultimate load method (ULM)

The method is based on the ultimate strength of reinforced concrete at ultimate load is

obtained by enhancing the service load by some factor called as load factor for giving a

desired margin of safety .Hence the method is also referred to as the load factor method or the

ultimate strength method.

In the ULM, stress condition at the state of in pending collapse of the structure is analysed,

thus using, the non-linear stress  strain curves of concrete and steel. The safely measure in

the design is obtained by the use of proper load factor. The satisfactory strength performance

at ultimate loads does not guarantee satisfactory strength performance at ultimate loads does

not guarantee satisfactory serviceability performance at normal service loads.

Limit state method (LSM)

Limit states are the acceptable limits for the safety and serviceability requirements of the

structure before failure occurs. The design of structures by this method will thus ensure that

they will not reach limit states and will not become unfit for the use for which they are

intended. It is worth mentioning that structures will not just fail or collapse by violating

(exceeding) the limit states. Failure, therefore, implies that clearly defined limit states of

structural usefulness has been exceeded.

Limit state are two types

i) Limit state of collapse

ii) Limit state of serviceability.

Limit states of collapse

The limit state of collapse of the structure or part of the structure could be assessed

from rupture of one or more critical sections and from bucking due to elastic bending, shear,

torsion and axial loads at every section shall not be less than the appropriate value at that

section produced by the probable most unfavourable combination of loads on the structure

using the appropriate factor of safely.

Limit state of serviceability

Limit state of serviceability deals with deflection and crocking of structures under service

loads, durability under working environment during their anticipated exposure conditions

during service, stability of structures as a whole, fire resistance etc.

Characteristic and design values and partial safety factor

1. Characteristic strength of materials.

  means that value of the strength of material below

which not more than minimum acceptable percentage of test results are expected to fall. IS

456:2000 have accepted the minimum acceptable percentage as 5% for reinforced concrete

structures. This means that there is 5% for probability or chance of the actual strength being

less than the characteristic strength.

Figure 1.4: Frequency distribution curve for strength

Figure shows frequency distribution curve of strength material (concrete or steel). The value

of K corresponding to 5% area of the curve is 1.65.

The design strength should be lower than the mean strength (f

m

)

Characteristic strength = Mean strength K x standard deviation or

f

k

=f

m

-KS

d

Where, f

k

=characteristic strength of the material

f

m

=mean strength

K=constant =1.65

S

d

=standard deviation for a set of test results.

The value of standard deviation (S

d

) is given by

2

1

d

S

n









Where, =deviation of the individual test strength from the average or mean strength of n

samples.

n= number of test results.

IS 456:2000 has recommended minimum value of n=30.

Characteristic strength of concrete

Characteristic strength of concrete is denoted by f

ck

(N/mm

2

) and its value is different for

different grades of concrete e.g. M 15, M25 designation of

concrete mix, refers to the mix and the number refers to the specified characteristic

compressive strength of 150 mm size cube at 28 days expressed in N/mm

2

Characteristic strength of steel

Until the relevant Indian Standard specification for reinforcing steel are modified to include

the concept of characteristic strength, the characteristic value shall be assumed as the

minimum yield stress or 0.2% proof stress specified in the relevant Indian Standard

specification. The characteristic strength of steel designated by symbol f

y

(N/mm

2

)

Characteristic loads



not being exceeded during that life of the structure.

Figure 1.5: Frequency distribution curve for load

The design load should be more than average load obtained from statistic, we have

F

k

=F

m

+KS

d

Where, F

k

=characteristic load;

F

m

= mean load

K=constant=2.65;

Sd=standard deviation for the load.

Since data are not available to express loads in statistical terms, for the purpose of this

standard, dead loads given in IS 875(Part-1), imposed loads given in IS 875(Part-2), wind

loads. Given in IS 875 (Part-3), snow load as given in IS 875(Part-4) and seismic forces given

in IS 1893 shall be assumed as the characteristic loads.

Design strength of materials

The design strength of materials (f

d

) is given by

k

d

m

f





Where, f

k

=characteristic strength of material.

m



=partial safety factor appropriate to the material and the limit state being

considered

Design loads

The design load ( F

d

) is given by.

F

d

=F

k

.

f



f



=partial safety factor appropriate to the nature of loading and the limit state being

considered.

The design load obtained by multi plying the characteristic load by the partial safety factor

for load is also known as factored load.

Partial safety factor (



m

) for materials

When assessing the strength of a structure or structural member for the limit state of collapse,

the values of partial safety factor,



m

should be taken as 1.15 for steel.

Thus, in the limit state method , the design stress for steel reinforcement is given by f

y

/



ms

=

f

y

/1.15=0.87f

y.

According to IS 456:2000 for design purpose the compressive strength of concrete in the

structure shall be assumed to be 0.67 times the characteristic strength of concrete in cube and

partial safety factor



mc

=1.5 shall be applied in addition to this. Thus, the design stress in

concrete is given by

0.67 / 0.67 /1.5 0.446

ck mc ck ck

f f f





Partial safety factor for loads

The partial safety factors for loads, as per IS 456:2000 are given in table below

Load

combination

Limit State of collapse

Limit State of Serviceability

DL

LL

WL/EL

DL

LL

WL/EL

DL+IL

1.5

-

1.0

-

DL+WL

1.5 or 0.9*

-

1.5

1.0

-

1.0

DL+IL+WL

1.2

1.0

0.8

(* This value is to be considered when stability against overturning or stress reversal is

critical)

Limit state of collapse in flexure

The behaviour of reinforced concrete beam sections at ultimate loads has been explained in

detail in previous section. The basic assumptions involved in the analysis at the ultimate limit

state of flexure (Cl. 38.1 of the Code) are listed here.

a) Plane sections normal to the beam axis remain plane after bending, i.e., in an initially

straight beam, strain varies linearly over the depth of the section.

b) The maximum compressive strain in concrete (at the outermost fibre)

cu



shall be taken as

0.0035 in bending.

c) The relationship between the compressive stress distribution in concrete and the strain in

concrete may be assumed to be rectangle, trapezoid, parabola or any other shape which

results in prediction of strength in substantial agreement with the results of test. An

acceptable stress-strain curve is given below in figure 1.6. For design purposes, the

compressive strength of concrete in the structure shall be assumed to be 0.67 times the

characteristic strength. The partial safety factor y, = 1.5 shall be applied in addition to this.

Figure 1.6 Stress-strain curve for concrete

d) The tensile strength of the concrete is ignored.

e) The stresses in the reinforcement are derived from representative stress-strain curve for the

type of steel used. Typical curves are given in figure 1.3. For design purposes the partial

safety factor

m



equal to 1.15 shall be applied.

f) The maximum strain in the tension reinforcement in the section at failure shall not be less

than:

0.002

1.15

y

s

f

E



Limiting Depth of Neutral Axis

Figure: 1.7 Rectangular beam under flexure

,maxuu

xx

Figure 1.8 Rectangular beam under flexure

,maxuu

xx

Based on the assumption given above, an expression for the depth of the neutral axis at the

ultimate limit state,

u

x

, can be easily obtained from the strain diagram in Fig. 1.8.

Considering similar triangles,

0.0035

0.87

0.0035 0.002

u

y

s

x

f

d

E





(1)

According to IS 456:2000 cl no 38.1 (f) ,when the maximum strain in tension reinforcement

is equal to

0.87

0.002

y

s

f

E



, then the value of neutral axis will be

,maxu

x

.

Therefore,

,max

0.0035

0.87

0.0035 0.002

u

y

s

x

f

d

E





(2)

The values of

,maxu

x

for different grades of steel, obtained by applying Eq. (2), are listed in

table.

Table 1 Limiting depth of neutral axis for different grades of steel

Steel Grade

Fe 250

Fe 415

Fe 500

,max

/

u

xd

0.5313

0.4791

The limiting depth of neutral axis

,maxu

x

corresponds to the so-called balanced section, i.e., a

tate in flexure. If

the neutral axis depth

u

x

is less than

,maxu

x

, then the section is under-reinforced (resulting in

    

u

x

exceeds

,maxu

x

, it is over-reinforced (resulting in a



Analysis of Singly Reinforced Rectangular Sections

Analysis of a given reinforced concrete section at the ultimate limit state of flexure implies

the determination of the ultimate moment M

uR

of resistance of the section. This is easily

obtained from the couple resulting from the flexural stresses (Fig 1.9).

Fig. 1.9 Concrete stress-block parameters in compression

..

uR u u

M C z T z



(3)

where

u

C

and

u

T

are the resultant (ultimate) forces in compression and tension respectively,

and z is the lever arm.

.

u st st

T f A

(4)

Where

,max

0.87

st y u u

f f for x x

and the line of action of T

u

corresponds to the level of the centroid of the tension steel.

Concrete Stress Block in Compression

In order to determine the magnitude of C

u

and its line of action, it is necessary to analyse the

concrete stress block in compression. As ultimate failure of a reinforced concrete beam in

flexure occurs by the crushing of concrete, for both under- and over-reinforced beams, the



shown in Fig. 1.9. The value of C

u

can be computed knowing that the compressive stress in

concrete is uniform at 0.447 f

ck

for a depth of 3x

u

/ 7, and below this it varies parabolically

over a depth of 4x

u

/ 7 to zero at the neutral axis [Fig. 1.9].

For a rectangular section of width b,

34

2

0.447 b

7 3 7

uu

u ck

xx

C f x















Therefore,

0.361

u ck u

C f bx

(5)

Also, the line of action of

u

C

is determined by the centroid of the stress block, located at a

distance

x

from the concrete fibres subjected to the maximum compressive strain.

Accordingly, considering moments of compressive forces C

u

, C

1

and C

2

[Fig. 1.9] about the

maximum compressive strain location,

1.5 4

3 2 4 5

(0.362 )x (0.447 ) x x

7 7 3 7 8 7

uu

ck u ck u u

xx

f bx x f bx x



   

  

   



   



Solving

0.416

u

xx

(6)

Depth of Neutral Axis

For any given section, the depth of the neutral axis should be such that

uu

CT

, satisfying

equilibrium of forces. Equating

uu

CT

, with expressions for

u

C

and

u

T

given by Eq. (5) and

Eq. (4) respectively.

0.87

0.361

y st

u

ck

fA

x

fb



, valid only if resulting

,maxuu

xx

(7)

Ultimate Moment of Resistance

The ultimate moment of resistance M

uR

of a given beam section is obtainable from Eq. (3).

The lever arm z, for the case of the singly reinforced rectangular section [Fig. 1.8, Fig. 1.9] is

given by

0.416

u

z d x

(8)

Accordingly, in terms of the concrete compressive strength,

0.361 (d 0.416x )

uR ck u u u

M f bx forall x

(9)

Alternatively, in terms of the steel tensile stress,

A (d 0.416x )

uR st st u u

M f forall x

(10)

With f

st

=0.87f

y

for

,maxuu

xx

Limiting Moment of Resistance

The limiting moment of resistance of a given (singly reinforced, rectangular) section,

 condition, defined by Eq. (2). From

Eq. (9), it follows that:

,lim ,max ,max

0.361 (d 0.416x )

u ck u u

M f bx

(11)

,max ,max

2

,lim

0.416x

0.361 1

uu

u ck

x

M f bd

dd

  



  

  

(11a)

Limiting Percentage Tensile Steel

Corresponding to the limiting moment of resistance

,limu

M

, there is a limiting percentage

tensile steel

,lim ,lim

100x /

t st

p A bd

. An expression for

,limt

p

is obtainable from Eq. (7) with:

,maxuu

xx

.

,max ,lim

0.87

x

0.361 100

y

ut

ck

f

xp

df



,max

,lim

41.61

u

ck

t

y

x

f

p

fd









(12)

The values of

,limt

p

and

2

u

M

bd

(in MPa units) for, different combinations of steel and

concrete grades are listed in Table 2. These values correspond to the so- 

section for a singly reinforced rectangular section.

Table 2 Limiting values of

,limt

p

and

2

u

M

bd

for singly reinforced rectangular beam sections for

various grades of steel and concrete.

(a)

,limt

p

values

M20

M25

M30

M35

M40

Fe 250

1.769

2.211

2.653

3.095

3.537

Fe 415

0.961

1.201

1.441

1.681

1.921

Fe 500

0.759

0.949

1.138

1.328

1.518

(a)

,lim

2

u

M

bd

values (MPa)

M20

M25

M30

M35

M40

Fe 250

2.996

3.746

4.495

5.244

5.993

Fe 415

2.777

3.472

4.166

4.860

5.555

Fe 500

2.675

3.444

4.013

4.682

5.350

Safety at Ultimate Limit State in Flexure

The bending moment expected at a beam section at the ultimate limit state due to the factored

loads is called the factored moment M

u

. For the consideration of various combinations of

loads (dead loads, live loads, wind loads, etc.), appropriate load factors should be applied to

M

u

is determined by structural

analysis.

         ng to the Code, if its ultimate

moment of resistance M

uR

is greater than or equal to the factored moment M

u

. In other words,

for such a design, the probability of failure is acceptably low. It is also the intention of the

Code to ensure that at ultimate failure in flexure, the type of failure should be a tension

(ductile) failure. For this reason, the Code requires the designer to ensure that

,maxuu

xx

,

whereby it follows that, for a singly reinforced rectangular section, the tensile reinforcement

percentage p

t

should not exceed

,limt

p

and the ultimate moment of resistance

uR

M

should not

exceed

,limu

M

.

Modes of failure: Types of section

A reinforced concrete member is considered to have failed when the strain of concrete in

extreme compression fibre reaches its ultimate value of 0.0035. At this stage, the actual strain

in steel can have the following values:

(a) Equal to failure strain of steel (

0.87

0.002

y

s

f

E



) corresponding to balanced section.

(b) More than failure strain, corresponding to under reinforced section.

(c) Less than failure strain corresponding to over reinforced section.

Thus for a given section, the actual value of

u

x

d

can be determined from Eq. (7). Three cases

may arise.

Case-1:

u

x

d

equal to the limiting value

,maxu

x

d

: Balanced section.

Case-2:

u

x

d

less than limiting value: under-reinforced section.

Case-3:

u

x

d

more than limiting value: over-reinforced section.

In balanced section, the strain in steel and strain in concrete reach their maximum values

simultaneously. The percentage of steel in this section is known as critical or limiting steel

percentage. The depth of neutral axis (NA) is

,maxuu

xx

.

Under-reinforced section

An under-reinforced section is the one in which steel percentage (pt) is less than critical or

limiting percentage (

,limt

p

). Due to this the actual NA is above the balanced NA and

,maxuu

xx

.

Over-reinforced section

In the over reinforced section the steel percentage is more than limiting percentage due to

which NA falls below the balanced NA and

,maxuu

xx

. Because of higher percentage of

steel, yield does not take place in steel and failure occurs when the strain in extreme fibres in

concrete reaches its ultimate value.

Computation of M

u

M

u

can be obtained by multiplying the tensile force T or the compressive force C with the

lever arm. The expressions of C, lever arm and T are given in Eqs. (4) and (3) respectively.

Previous section discusses that there are three possible cases depending on the location of x

u

.

The corresponding expressions of M

u

are given below for the three cases:

(i) When x

u

< x

u, max

In this case the concrete reaches 0.0035, steel has started flowing showing ductility (Strain >

0.87

0.002

y

s

f

E



). So, the computation of M

u

is to be done using the tensile force of steel in

this case.

Therefore, M

u

= T (lever arm) = 0.87 f

y

A

st

(d - 0.42 x

u

)

(ii) When x

u

= x

u, max

In this case steel just reaches the value of

0.87

0.002

y

s

f

E



and concrete also reaches its

maximum value. The strain of steel can further increase but the reaching of limiting strain of

concrete should be taken into consideration to determine the limiting M

u

as M

u, lim

here. So,

we have

M

u, lim

= C (lever arm)

Substituting the expressions of C

,max ,max

2

,lim

0.36 1 0.42

uu

u ck

xx

M f bd

dd









(iii) When x

u

> x

u, max

In this case, concrete reaches the strain of 0.0035, tensile strain of steel is much less than (

0.87

0.002

y

s

f

E



) and any further increase of strain of steel will mean failure of concrete,

which is to be avoided. On the other hand, when steel reaches

0.87

0.002

y

s

f

E



, the strain of

concrete far exceeds 0.0035. Hence, it is not possible. Therefore, such design is avoided and

the section should be redesigned.

However, in case of any existing reinforced concrete beam where x

u

> x

u, max

, the moment of

resistance M

u

for such existing beam is calculated by restricting x

u

to x

u, max

only and the

corresponding M

u

will be as per the case when x

u

= x

u, max

.

Numerical Problem

Find the moment of resistance of a singly reinforced concrete beam of 200 mm width 400mm

effective depth, reinforced with 3-16 mm diameter bars of Fe 415 steel. Take M20 grade of

concrete.

Solution

22

3 (16) 603.19

4

603.19

% 100 0.754%

200 400

st

t

A x mm

px

x





0.754 415

2.417 2.417 0.378

100 20

y

u

t

ck

f

x

p x x

df

  

Now for Fe 415 grade of steel,

,max

0.479

u

x

d



Hence the beam is under-reinforced.

The moment of resistance is given by

0.87 1

y st

u y st

ck

fA

M f A d

f bd









415 603.19

0.87 415 603.19 400 1

20 200 400

x

x x x

xx









=73.48 KN-m.

Design Type of Problems

The designer has to make preliminary plan lay out including location of the beam, its span

and spacing, estimate the imposed and other loads from the given functional requirement of

the structure. The dead loads of the beam are estimated assuming the dimensions b and d

initially. The bending moment, shear force and axial thrust are determined after estimating

the different loads. In this illustrative problem, let us assume that the imposed and other loads

are given. Therefore, the problem is such that the designer has to start with some initial

dimensions and subsequently revise them, if needed. The following guidelines are helpful to

assume the design parameters initially.

(i) Selection of breadth of the beam b

Normally, the breadth of the beam b is governed by: (i) proper housing of reinforcing bars

and (ii) architectural considerations. It is desirable that the width of the beam should be less

than or equal to the width of its supporting structure like column width, or width of the wall

etc. Practical aspects should also be kept in mind. It has been found that most of the

requirements are satisfied with b as 150, 200, 230, 250 and 300 mm. Again, width to overall

depth ratio is normally kept between 0.5 and 0.67.

(ii) Selection of depths of the beam d and D

The effective depth has the major role to play in satisfying (i) the strength requirements of

bending moment and shear force, and (ii) deflection of the beam. The initial effective depth

of the beam, however, is assumed to satisfy the deflection requirement depending on the span

and type of the reinforcement. IS 456 stipulates the basic ratios of span to effective depth of

beams for span up to 10 m as (Clause 23.2.1)

Cantilever 7

Simply supported 20

Continuous 26

For spans above 10 m, the above values may be multiplied with 10/span in metres, except for

cantilevers where the deflection calculations should be made. Further, these ratios are to be

multiplied with the modification factor depending on reinforcement percentage and type.

Figures 4 and 5 of IS 456 give the different values of modification factors. The total depth D

can be determined by adding 40 to 80 mm to the effective depth.

(iii) Selection of the amount of steel reinforcement A

st

The amount of steel reinforcement should provide the required tensile force T to resist the

factored moment M

u

of the beam. Further, it should satisfy the minimum and maximum

percentages of reinforcement requirements also. The minimum reinforcement A

s

is provided

for creep, shrinkage, thermal and other environmental requirements irrespective of the

strength requirement. The minimum reinforcement A

s

to be provided in a beam depends on

the f

y

of steel and it follows the relation: (cl. 26.5.1.1a of IS 456)

0.85

s

y

A

bd f



The maximum tension reinforcement should not exceed 0.04 bD (cl. 26.5.1.1b of IS 456),

where D is the total depth.

Besides satisfying the minimum and maximum reinforcement, the amount of reinforcement

of the singly reinforced beam should normally be 75 to 80% of p

t, lim

. This will ensure that

strain in steel will be more than (

0.87

0.002

y

s

f

E



) as the design stress in steel will be 0.87 f

y

.

Moreover, in many cases, the depth required for deflection becomes more than the limiting

depth required to resist M

u, lim

. Thus, it is almost obligatory to provide more depth. Providing

more depth also helps in the amount of the steel which is less than that required for M

u, lim

.

This helps to ensure ductile failure. Such beams are designated as under-reinforced beams.

(iv) Selection of diameters of bar of tension reinforcement

Reinforcement bars are available in different diameters such as 6, 8, 10, 12, 14, 16, 18, 20,

22, 25, 28, 30, 32, 36 and 40 mm. Some of these bars are less available. The selection of the

diameter of bars depends on its availability, minimum stiffness to resist while persons walk

over them during construction, bond requirement etc. Normally, the diameters of main tensile

bars are chosen from 12, 16, 20, 22, 25 and 32 mm.

(v) Selection of grade of concrete

Besides strength and deflection, durability is a major factor to decide on the grade of

concrete. Table 5 of IS 456 recommends M 20 as the minimum grade under mild

environmental exposure and other grades of concrete under different environmental

exposures also.

(vi) Selection of grade of steel

Normally, Fe 250, 415 and 500 are in used in reinforced concrete work. Mild steel (Fe 250) is

more ductile and is preferred for structures in earthquake zones or where there are

possibilities of vibration, impact, blast etc.

Failure Modes due to Shear

Figure 1.10 (a) Web shear progress along dotted lines

Figure 1.10 (b) Flexural tension

Figure 1.10 (b) Flexural compression

Bending in reinforced concrete beams is usually accompanied by shear, the exact analysis of

which is very complex. However, experimental studies confirmed the following three

different modes of failure due to possible combinations of shear force and bending moment at

a given section:

(i) Web shear (Fig. 1.10a)

(ii) Flexural tension shear (Fig. 1.10b)

(iii) Flexural compression shear (Fig. 1.10c)

Web shear causes cracks which progress along the dotted line shown in Fig. 1.10a. Steel

yields in flexural tension shear as shown in Fig. 1.10b, while concrete crushes in compression

due to flexural compression shear as shown in Fig. 1.10c. An in-depth presentation of the

three types of failure modes is beyond the scope here. Only the salient points needed for the

routine design of beams in shear are presented here.

Shear Stress

The distribution of shear stress in reinforced concrete rectangular, T and L-beams of uniform

and varying depths depends on the distribution of the normal stress. However, for the sake of

simplicity the nominal shear stress τ

v

is considered which is calculated as follows (IS 456, cls.

40.1 and 40.1.1):

Figure 1.11: Distribution of shear stress and average shear stress

(i) In beams of uniform depth (Figs. 1.11a and b):

u

v

V

bd





(13)

where V

u

= shear force due to design loads,

b = breadth of rectangular beams and breadth of the web b

w

for flanged beams, and

d = effective depth.

(ii) In beams of varying depth:

tan

u

v

M

V

d

bd









(14)



v

, Vu, b or b

w

and d are the same as in (i),

M

u

= bending moment at the section, and



The positive sign is applicable when the bending moment M

u

decreases numerically in the

same direction as the effective depth increases, and the negative sign is applicable when the

bending moment M

u

increases numerically in the same direction as the effective depth

increases.

Design Shear Strength of Reinforced Concrete

Recent laboratory experiments confirmed that reinforced concrete in beams has shear strength

even without any shear reinforcement. This shear strength (τ

c

) depends on the grade of concrete

and the percentage of tension steel in beams. On the other hand, the shear strength of reinforced

concrete with the reinforcement is restricted to some maximum value τ

cmax

depending on the

grade of concrete. These minimum and maximum shear strengths of reinforced concrete (IS 456,

cls. 40.2.1 and 40.2.3, respectively) are given below:

Design shear strength without shear reinforcement (IS 456, cl. 40.2.1)

Table 19 of IS 456 stipulates the design shear strength of concrete τ

c

for different grades of

concrete with a wide range of percentages of positive tensile steel reinforcement. It is worth

mentioning that the reinforced concrete beams must be provided with the minimum shear

reinforcement as per cl. 40.3 even when τ

v

is less than τ

c

given in Table 3.

Table 3 Design shear strength of concrete, τ

c

in N/mm

2

100 /

s

A bd

Grade of concrete

M 20

M 25

M 30

M 35

M40 and

above

≤ 0.15

0.25

0.50

0.28

0.36

0.48

0.29

0.36

0.49

0.29

0.37

0.50

0.29

0.37

0.50

0.30

0.38

0.51

0.75

0.56

0.57

0.59

0.60

1.00

1.25

0.62

0.67

0.64

0.70

0.66

0.71

0.67

0.73

0.68

0.74

1.50

1.75

2.00

0.72

0.75

0.79

0.74

0.78

0.82

0.76

0.80

0.84

0.78

0.82

0.86

0.79

0.84

0.88

2.25

2.50

2.75

≥ 3.00

0.81

0.82

0.85

0.88

0.90

0.92

0.88

0.91

0.94

0.96

0.90

0.93

0.96

0.99

0.92

0.95

0.98

1.01

In Table 3, A

s

is the area of longitudinal tension reinforcement which continues at least one

effective depth beyond the section considered except at support where the full area of tension

reinforcement may be used provided the detailing is as per IS 456, cls. 26.2.2 and 26.2.3.

Maximum shear stress τ

cmax

with shear reinforcement (cls. 40.2.3, 40.5.1 and 41.3.1)

Table 20 of IS 456 stipulates the maximum shear stress of reinforced concrete in beams τ

cmax

as given below in Table 6.2. Under no circumstances, the nominal shear stress in beams τ

v

shall exceed τ

cmax

given in Table 6.2 for different grades of concrete.

Table 4 Maximum shear stress, τ

cmax

in N/mm

2

Grade of

concrete

M 20

M 25

M 30

M 35

M 40 and

above

,maxc



N/mm

2

2.8

3.1

3.5

3.7

4.0

Critical Section for Shear

Figure 1.12 Support condition for locating factored shear force

Clauses 22.6.2 and 22.6.2.1 stipulate the critical section for shear and are as follows:

For beams generally subjected to uniformly distributed loads or where the principal load is

located further than 2d from the face of the support, where d is the effective depth of the

beam, the critical sections depend on the conditions of supports as shown in Figs. 1.12 a, b

and c and are mentioned below.

(i) When the reaction in the direction of the applied shear introduces tension (Fig. 1.12a) into

the end region of the member, the shear force is to be computed at the face of the support of

the member at that section.

(ii) When the reaction in the direction of the applied shear introduces compression into the

end region of the member (Figs. 1.12b and c), the shear force computed at a distance d from

the face of the support is to be used for the design of sections located at a distance less than d

from the face of the support. The enhanced shear strength of sections close to supports,

however, may be considered as discussed in the following section.

Minimum Shear Reinforcement (cls. 40.3, 26.5.1.5 and 26.5.1.6 of IS 456)

Minimum shear reinforcement has to be provided even when τ

v

is less than τ

c

given in Table 3

as recommended in cl. 40.3 of IS 456. The amount of minimum shear reinforcement, as given

in cl. 26.5.1.6, is given below.

The minimum shear reinforcement in the form of stirrups shall be provided such that:

0.4

0.87

sv

vy

A

bs f



(15)

where A

sv

= total cross-sectional area of stirrup legs effective in shear,

s

v

= stirrup spacing along the length of the member,

b = breadth of the beam or breadth of the web of the web of flanged beam b

w

, and

f

y

= characteristic strength of the stirrup reinforcement in N/mm

2

which shall not be

taken greater than 415 N/mm

2

.

The above provision is not applicable for members of minor structural importance such as

lintels where the maximum shear stress calculated is less than half the permissible value.

The minimum shear reinforcement is provided for the following:

(i) Any sudden failure of beams is prevented if concrete cover bursts and the bond to

the tension steel is lost.

(ii) Brittle shear failure is arrested which would have occurred without shear

reinforcement.

(iii) Tension failure is prevented which would have occurred due to shrinkage,

thermal stresses and internal cracking in beams.

(iv) To hold the reinforcement in place when concrete is poured.

(v) Section becomes effective with the tie effect of the compression steel.

Further, cl. 26.5.1.5 of IS 456 stipulates that the maximum spacing of shear reinforcement

measured along the axis of the member shall not be more than 0.75 d for vertical stirrups and

d for inclined stirrups at 45

o

, where d is the effective depth of the section. However, the

spacing shall not exceed 300 mm in any case.

Design of Shear Reinforcement (cl. 40.4 of IS 456)

When τ

v

is more than τ

c

given in Table 6.1, shear reinforcement shall be provided in any of

the three following forms:

(a) Vertical stirrups,

(b) Bent-up bars along with stirrups, and

(c) Inclined stirrups.

In the case of bent-up bars, it is to be seen that the contribution towards shear resistance of

bent-up bars should not be more than fifty per cent of that of the total shear reinforcement.

The amount of shear reinforcement to be provided is determined to carry a shear force V

us

equal to

us u c

V V bd





(16)

where b is the breadth of rectangular beams or b

w

in the case of flanged beams.

The strengths of shear reinforcement V

us

for the three types of shear reinforcement are as

follows:

(a) Vertical stirrups:

0.87

y sv

us

v

f A d

V

s



(17)

(b) For inclined stirrups or a series of bars bent-up at different cross-sections:

0.87

(sin cos )

y sv

us

v

f A d

V

s





(18)

(c) For single bar or single group of parallel bars, all bent-up at the same cross-section:

0.87 sin

us y sv

V f A d





(19)

where A

sv

= total cross-sectional area of stirrup legs or bent-up bars within a distance s

v

,

s

v

= spacing of stirrups or bent-up bars along the length of the member,



v

= nominal shear stress,



c

= design shear strength of concrete,

b = breadth of the member which for the flanged beams shall be taken as the breadth

of the web b

w

,

f

y

= characteristic strength of the stirrup or bent-up reinforcement which shall not be

taken greater than 415 N/mm

2

,

-up bar and the axis of the member, not

less than 45

o

, and

d = effective depth.

The following two points are to be noted:

(i) The total shear resistance shall be computed as the sum of the resistance for the

various types separately where more than one type of shear reinforcement is

used.

(ii) The area of stirrups shall not be less than the minimum specified in cl. 26.5.1.6.

Curtailment of Tension Reinforcement in Flexural Members (cl. 26.2.3.2 of IS 456)

Curtailment of tension reinforcement is done to provide the required reduced area of steel

with the reduction of the bending moment. However, shear force increases with the reduction

of bending moment. Therefore, it is necessary to satisfy any one of following three conditions

while terminating the flexural reinforcement in tension zone:



v

at the cut-off point should not exceed two-thirds of the permitted value

which includes the shear strength of the web reinforcement. Accordingly,

(2 /3)( / )

(1.5 )

v c us

us v c

V bd

or V bd







(ii) For each of the terminated bars, additional stirrup area should be provided over a distance

of three-fourth of effective depth from the cut-off point. The additional stirrup area shall not

be less than 0.4 b s/f

y

, where b is the breadth of rectangular beams and is replaced by b

w

, the

breadth of the web for flanged beams, s = spacing of additional stirrups and f

y

is the

characteristic strength of stirrup reinforcement in N/mm

2

. The value of s shall not exceed d/(8



b

), where 

b

is the ratio of area of bars cut-off to the total area of bars at that section, and d is

the effective depth.

(iii) For bars of diameters 36 mm and smaller, the continuing bars provide double the area

required for flexure at the cut-off point. The shear stress should not exceed three-fourths that

permitted. Accordingly,

(3/ 4)( / )

(1.33 )

v c us

us v c

V bd

or V bd







In the above expression b is the breadth of the rectangular beams which will be b

w

in the case

of flanged beams.

Bond

The bond between steel and concrete is very important and essential so that they can act

together without any slip in a loaded structure. With the perfect bond between them, the plane

section of a beam remains plane even after bending. The length of a member required to

develop the full bond is called the anchorage length. The bond is measured by bond stress.

The local bond stress varies along a member with the variation of bending moment.

Thus, a tensile member has to be anchored properly by providing additional length on either

side of the point 

L

d



Accordingly, IS 456, cl. 26.2 stipulates the requirements of proper anchorage of

reinforcement in terms of development length L

d



bd

.

Design bond stress – values

The average bond stress is still used in the working stress method and IS 456 has mentioned

about it in cl. B-2.1.2. However, in the limit state method of design, the average bond stress



bd

and the values are given in cl. 26.2.1.1. The

same is given below as a ready reference.



bd

for plain bars in tension

Grade of concrete

M 20

M 25

M 30

M 35

M 40 and

above

Design Bond Stress

τ

bd

in N/mm2

1.2

1.4

1.5

1.7

1.9

For deformed bars conforming to IS 1786, these values shall be increased by 60 per cent. For

bars in compression, the values of bond stress in tension shall be increased by 25 per cent.

Development Length

Figure 1.13 Development length of bar

Figure 1.13 shows the free body diagram of the segment AB of the bar. At B, the tensile force T

trying to pull out the bar is of the value T 

2



s





s

is the tensile stress in bar at the section considered at design loads. It is necessary to have



bd

for the length L

d

to overcome the tensile force. The

L

d



bd

). Equating the two, we get

L

d



bd



2



s

/4) (19)

Equation (19), thus gives

4

s

d

bd

L







(20)

The above equation is given in cl. 26.2.1 of IS 456 to determine the development length of

bars.

The example taken above considers round bar in tension. Similarly, other sections of the bar

should have the required L

d

as determined for such sections. For bars in compression, the



bd

is

25 per cent more than that in tension (see the last lines below Table 6.4). Following the same

logic, the development length of deformed bars is reduced by 60 per cent of that needed for

the plain round bars. Tables 64 to 66 of SP-16 present the development lengths of fully



s

= 0.87 f

y

) both under tension and compression. It is

to be noted that the consequence of stress concentration at the lugs of deformed bars has not

been taken into consideration.

Checking of Development Lengths of Bars in Tension

The following are the stipulation of cl. 26.2.3.3 of IS 456.

(i) At least one-third of the positive moment reinforcement in simple members and one-fourth

of the positive moment reinforcement in continuous members shall be extended along the

same face of the member into the support, to a length equal to L

d

/3.

(ii) Such reinforcements of (i) above shall also be anchored to develop its design stress in

tension at the face of the support, when such member is part of the primary lateral load

resisting system.

(iii) The diameter of the positive moment reinforcement shall be limited to a diameter such

that the L

d



s

= f

d

in Eq. (20) does not exceed the following:

1

0

()

sd

d when f

M

LL

V







(21)

where M

1

= moment of resistance of the section assuming all reinforcement at the section to

be stressed to fd,

f

d

= 0.87 fy,

V = shear force at the section due to design loads,

L

o

= sum of the anchorage beyond the centre of the support and the equivalent

anchorage value of any hook or mechanical anchorage at simple support. At

a point of inflection, L

o

is limited to the effective depth of the member or





It has been further stipulated that M

1

/V in the above expression may be increased by 30 per

cent when the ends of the reinforcement are confined by a compressive reaction.

Numerical problem of design of singly reinforced beam

A reinforced concrete beam is supported on two walls 250mm thick, spaced at a clear

distance of 6m. The beam carries a super-imposed load of 9.8 KN/m. design the beam using

M20 concrete and HYSD bars of Fe 415 grade.

Solution

The minimum depth of beam is based on limit state of serviceability requirements.

As per IS 456:2000 cl no 23.2.1 (a), for simply supported beam l/d=20 and for balanced

section,

,lim

0.96%

t

p

Also for Fe 415 steel, f

s

=0.58x415=240 N/mm

2

As per IS 456:2000 cl no 23.2.1(c) and fig 4 of IS 456:2000 modification factor=1.

Therefore, l/d=20x1;

/ 20 6000/ 20 300dl   

This is the minimum value of d. actual value of d, based on bending may be more than this.

Now from experience, assume d=l/15=400mm

Therefore, overall depth= effective depth+ clear cover + diameter of stirrup +0.5(diameter of

main reinforcement)

=400+25+8+0.5x20=443mm

450mm

Assume b=250mm

Therefore, try a trial section of dimension 250x450.

Load Calculation

Self-weight of beam (DL)= 0.25x0.45x1x25=2.8125 KN/m

Super-imposed load (LL)= 9.8 KN/m

Therefore, total load,

w

=(DL+LL)=(2.8125+9.8)=12.6125 KN/m

Design load,

u

w

=1.5x

w

=18.9187 KN/m

Calculation of effective span

As per IS 456:2000, cl no 22.2 (a), the effective span of a simply supported beam is lesser of

the following two.

Clear span+ the effective depth of beam or slab

Or centre to centre distance between supports.

Clear span =6m

Effective depth of beam, d=450-25-8-0.5x20=407mm

Therefore, clear span + effective depth of beam=(6+0.407)m=6.407m

Centre to centre distance between support=(6+0.25/2+0.25/2)m=6.25m

Lesser of two=6.25m

Therefore, effective span =6.25m

Calculation of BM and SF

Maximum BM =

2

18.9187 6.25

92.376

88

u

wl

x

KN m  

Maximum SF=

18.9187 6.25

59.12

22

u

wl

x

KN

Computation of effective depth, d

For M20 grade of concrete and Fe 415 grade of steel

2

0.138

u ck

M f bd

Therefore, d=

6

92.376 10

365.89

0.138 20 250

x

mm

xx



Now assumed depth was =407mm

Therefore, r

equired

< a

ssumed

So, the section assumed is safe from bending moment point of view.

Since the available depth (407mm) is greater than required depth (365.89mm). So the section

is under reinforced.

Calculation of steel reinforcement

The reinforcement for an under-reinforced section is given by

Ast=

6

22

0.5 4.6

0.5 20 4.6 92.376 10

1 1 1 1 (250 407)

415

20 250 407

ck u

y

ck

fM

x x x

bd x

f

f bd x x





    





A

st

=740.88mm

2

%pt=

740.88

100 0.728%

250 407x



<

,limt

p

Therefore, using 20 mm dia, no of bars required =

740.88

2.35 3.

(20)

4





Provide 3nos 20 diameter bar.

Shear Reinforcement



face of the support.

So, shear force at that distance, V

u

=59.12-18.9187(0.25/2+0.407) = 49.05 KN.

Nominal shear stress,

3

2

49.05 10

0.482 /

250 407

u

v

V

x

N mm

bd x



  

% p

t

at support =

2

3 (20)

4

100 0.926%

250 407

x





As per IS 456:2000, table 19, the design shear strength of concrete,

c



for %pt=0.926 and

M20 grade of concrete,

2

0.61 /

c

N mm





Since

vc





, no shear reinforcement is necessary. However, minimum shear reinforcement

as per cl no 26.5.1.6 of IS 456:2000 should be provided.

2.175

0.4

0.87

sv y

sv

v

vy

Af

A

S

bS f b

  

As per cl no 26.5.1.5 of IS 456:2000, maximum spacing of shear reinforcement least of the

following

(a) 0.75d or (b) 300mm

Hence provide 2

L

-8 mm diameter @ 300mm c/c throughout the length of the beam.

Check for Development length

As per cl no 26.2.1 of IS 456:2000, the development length L

d

is given by

4

s

d

bd

L







bd



=1.2 N/mm

2

for M20 grade of concrete.

For deformed bars conforming to Is 1786 these values shall be increased by 60%.

20 0.87 415

940.23

(4 ) 1.6 4 1.2 1.6

s

d

bd

xx

L mm

x x x





  

Now as per cl no 26.2.3.3 (c) of IS 456:2000, at a simple support and at points of inflection,

positive moment tension reinforcement shall be limited to a diameter such that L

d

computed

for f

d

does not exceed

1

0

M

L

V



The value of

1

M

V

in the above expression may be increased by 30% when the ends of the

reinforcement are confined by a compressive reaction.

1

0

1.3

d

M

LL

V



3 bars are available at supports.

.87

0.87 415 (3 314.15)

189

0.36 0.36 20 250

y st

u

ck

o f A

x x x

x mm

f b x x

  

1

0.87 ( 0.416 )

0.87 415 (3 314.15)(407 0.416 189)

111.73

y st u

M f A d x

x x x x

KN m



V=59.12 KN

L

0

= greatest of effective depth of member or 12



=407mm

1

0

1.3 2.863

M

Lm

V



Therefore,

1

0

1.3

d

M

LL

V



Reinforcement Detailing

6 m

3-20

2-10

450mm

2-10

2

L

-8 @ 300c/c

2

L

-8 @ 300c/c

MODULE-2

One-way and Two-way Slabs

Figure 2.1(a) One-way slab (l

y

/l

x

>2)

Figure 2.1(b) Two-way slab (l

y

/l

x

<=2)

Figures 2.1a and b explain the share of loads on beams supporting solid slabs along four

edges when vertical loads are uniformly distributed. It is evident from the figures that the

share of loads on beams in two perpendicular directions depends upon the aspect ratio l

y

/l

x

of

the slab, l

x

being the shorter span. For large values of l

y

, the triangular area is much less than

the trapezoidal area (Fig. 2.1a). Hence, the share of loads on beams along shorter span will

gradually reduce with increasing ratio of l

y

/l

x

. In such cases, it may be said that the loads are

primarily taken by beams along longer span. The deflection profiles of the slab along both

directions are also shown in the figure. The deflection profile is found to be constant along

the longer span except near the edges for the slab panel of Fig. 2.1a. These slabs are

designated as one-way slabs as they span in one direction (shorter one) only for a large part

of the slab when l

y

/l

x

> 2.

On the other hand, for square slabs of l

y

/l

x

= 1 and rectangular slabs of l

y

/l

x

up to 2, the

deflection profiles in the two directions are parabolic (Fig. 2.1b). Thus, they are spanning in

two directions and these slabs with l

y

/l

x

up to 2 are designated as two-way slabs, when

supported on all edges.

It would be noted that an entirely one-way slab would need lack of support on short edges.

Also, even for l

y

/l

x

< 2, absence of supports in two parallel edges will render the slab one-

way. In Fig. 2.1b, the separating line at 45 degree is tentative serving purpose of design.

Actually, this angle is a function of l

y

/l

x

.

Design of One-way Slabs

The procedure of the design of one-way slab is the same as that of beams. However, the amounts

of reinforcing bars are for one metre width of the slab as to be determined from either the

governing design moments (positive or negative) or from the requirement of minimum

reinforcement. The different steps of the design are explained below.

Step 1: Selection of preliminary depth of slab

The depth of the slab shall be assumed from the span to effective depth ratios.

Step 2: Design loads, bending moments and shear forces

The total factored (design) loads are to be determined adding the estimated dead load of the slab,

load of the floor finish, given or assumed live loads etc. after multiplying each of them with the

respective partial safety factors. Thereafter, the design positive and negative bending moments

and shear forces are to be determined using the respective coefficients given in Tables 12 and 13

of IS 456.

Step 3: Determination/checking of the effective and total depths of slabs

The effective depth of the slab shall be determined employing.

M

u,lim

= R

,lim

bd

2

The total depth of the slab shall then be determined adding appropriate nominal cover (Table 16

and 16A of cl.26.4 of IS 456) and half of the diameter of the larger bar if the bars are of different

sizes. Normally, the computed depth of the slab comes out to be much less than the assumed

depth in Step 1. However, final selection of the depth shall be done after checking the depth for

shear force.

Step 4: Depth of the slab for shear force

Theoretically, the depth of the slab can be checked for shear force if the design shear strength of

concrete is known. Since this depends upon the percentage of tensile reinforcement, the design

shear strength shall be assumed considering the lowest percentage of steel. The value of

c



shall

be modified after knowing the multiplying factor k from the depth tentatively selected for the slab

in Step 3. If necessary, the depth of the slab shall be modified.

Step 5: Determination of areas of steel

Area of steel reinforcement along the direction of one-way slab should be determined

employing the following Eq.

M

u

= 0.87 f

y

A

st

d {1  (A

st

)(f

y

)/(f

ck

)(bd)}

The above equation is applicable as the slab in most of the cases is under-reinforced due to

the selection of depth larger than the computed value in Step 3. The area of steel so

determined should be checked whether it is at least the minimum area of steel as mentioned

in cl.26.5.2.1 of IS 456.

Step 6: Selection of diameters and spacings of reinforcing bars (cls.26.5.2.2 and 26.3.3 of

IS 456)

The diameter and spacing of bars are to be determined as per cls.26.5.2.2 and 26.3.3 of IS

456. As mentioned in Step 5, this step may be avoided when using the tables and charts of

SP-16.

Design the one-way continuous slab of Fig.8.18.6 subjected to uniformly distributed imposed

loads of 5 kN/m

2

using M 20 and Fe 415. The load of floor finish is 1 kN/m

2

. The span

dimensions shown in the figure are effective spans. The width of beams at the support = 300

mm.

Step 1: Selection of preliminary depth of slab

The basic value of span to effective depth ratio for the slab having simple support at the end

and continuous at the intermediate is (20+26)/2 = 23 (cl.23.2.1 of IS 456).

Modification factor with assumed p = 0.5 and f

s

= 240 N/mm

2

is obtained as 1.18 from Fig.4

of IS 456.

Therefore, the minimum effective depth = 3000/23(1.18) = 110.54 mm. Let us take the

effective depth d = 115 mm and with 25 mm cover, the total depth D = 140 mm.

Step 2: Design loads, bending moment and shear force

Dead loads of slab of 1 m width = 0.14(25) = 3.5 kN/m

Dead load of floor finish =1.0 kN/m

Factored dead load = 1.5(4.5) = 6.75 kN/m

Factored live load = 1.5(5.0) = 7.50 kN/m

Total factored load = 14.25 kN/m

Maximum moments and shear are determined from the coefficients given in Tables 12 and 13

of IS 456.

Maximum positive moment = 14.25(3)(3)/12 = 10.6875 kNm/m

Maximum negative moment = 14.25(3)(3)/10 = 12.825 kNm/m

Maximum shear V

u

= 14.25(3)(0.4) = 17.1 kN

Step 3: Determination of effective and total depths of slab

From Eq. M

u,lim

= R

,lim

bd

2

where R

,lim

is 2.76 N/mm

2

. So, d = {12.825(10

6

)/(2.76)(1000)}

0.5

=

68.17 mm

Since, the computed depth is much less than that determined in Step 1, let us keep D = 140

mm and d = 115 mm.

Step 4: Depth of slab for shear force

Table 19 of IS 456 gives

c



= 0.28 N/mm

2

for the lowest percentage of steel in the slab.

Further for the total depth of 140 mm, let us use the coefficient k of cl. 40.2.1.1 of IS 456 as

1.3 to get

cc

k





= 1.3(0.28) = 0.364 N/mm

2

.

Table 20 of IS 456 gives

,maxc



= 2.8 N/mm

2

. For this problem

u

v

V

bd





bdVuv  

17.1/115 = 0.148 N/mm

2

. Since,

,maxvcc





, the effective depth d = 115 mm is

acceptable.

Step 5: Determination of areas of steel

It is known that

M

u

= 0.87 f

y

A

st

d {1  (A

st

)(f

y

)/(f

ck

)(bd)}

(i) For the maximum negative bending moment

12825000 = 0.87(415)(A

st

)(115){1  (A

st

)(415)/(1000)(115)(20)}

or - 5542.16 A2stA

st

+ 1711871.646 = 0

Solving the quadratic equation, we have the negative A

st

= 328.34 mm

2

(ii) For the maximum positive bending moment

10687500 = 0.87(415) A

st

(115) {1  (A

st

)(415)/(1000)(115)(20)}

or - 5542.16 A2stA

st

+ 1426559.705 = 0

Solving the quadratic equation, we have the positive A

st

= 270.615 mm

2

Distribution steel bars along longer span l

y

Distribution steel area = Minimum steel area = 0.12(1000)(140)/100 = 168 mm

2

. Since, both

positive and negative areas of steel are higher than the minimum area, we provide:

(a) For negative steel: 10 mm diameter bars @ 230 mm c/c for which A

st

= 341 mm

2

giving p

s

= 0.2965.

(b) For positive steel: 8 mm diameter bars @ 180 mm c/c for which A

st

= 279 mm

2

giving p

s

= 0.2426

(c) For distribution steel: Provide 8 mm diameter bars @ 250 mm c/c for which A

st

(minimum) = 201 mm

2

.

Step 6: Selection of diameter and spacing of reinforcing bars

The diameter and spacing already selected in step 5 for main and distribution bars are

checked below:

For main bars (cl. 26.3.3.b.1 of IS 456), the maximum spacing is the lesser of 3d and 300 mm

i.e., 300 mm. For distribution bars (cl. 26.3.3.b.2 of IS 456), the maximum spacing is the

lesser of 5d or 450 mm i.e., 450 mm. Provided spacings, therefore, satisfy the requirements.

Maximum diameter of the bars (cl. 26.5.2.2 of IS 456) shall not exceed 140/8 = 17 mm is

also satisfied with the bar diameters selected here.

Two-way Slabs

Two-way slabs subjected mostly to uniformly distributed loads resist them primarily by

bending about both the axis. However, as in the one-way slab, the depth of the two-way slabs

should also be checked for the shear stresses to avoid any reinforcement for shear. Moreover,

these slabs should have sufficient depth for the control deflection. Thus, strength and

deflection are the requirements of design of two-way slabs.

Figure 2.2 strips for shear

Computation of shear force

Shear forces are computed following the procedure stated below with reference to

Fig.2.2.

The two-way slab of Fig. 2.2 is divided into two trapezoidal and two triangular zones by

drawing lines from each corner at an angle of 45

o

. The loads of triangular segment A will be

transferred to beam 1-2 and the same of trapezoidal segment B will be beam 2-3. The shear

forces per unit width of the strips aa and bb are highest at the ends of strips. Moreover, the

length of half the strip bb is equal to the length of the strip aa. Thus, the shear forces in both

strips are equal and we can write,

V

u

= W (l

x

/2)

where W = intensity of the uniformly distributed loads.

The nominal shear stress acting on the slab is then determined from

u

v

V

bd





Computation of bending moments

Two-way slabs spanning in two directions at right angles and carrying uniformly distributed

-

st commonly used in

the limit state of collapse method and suggested by IS 456 in the note of cl. 24.4.

Alternatively, Annex D of IS 456 can be employed to determine the bending moments in the

two directions for two types of slabs: (i) restrained slabs, and (ii) simply supported slabs. The

two methods are explained below:

(i) Restrained slabs

Restrained slabs are those whose corners are prevented from lifting due to effects of torsional

moments. These torsional moments, however, are not computed as the amounts of

reinforcement are determined from the computed areas of steel due to positive bending

moments depending upon the intensity of torsional moments of different corners. Thus, it is

essential to determine the positive and negative bending moments in the two directions of

restrained slabs depending on the various types of panels and the aspect ratio l

y

/l

x

.

Figure 2.3 (a): For Span l

x

Figure 2.3 (b): For Span l

y

Restrained slabs are considered as divided into two types of strips in each direction: (i) one

middle strip of width equal to three-quarters of the respective length of span in either

directions, and (ii) two edge strips, each of width equal to one-eighth of the respective length

of span in either directions. Figures 2.3 (a) and b present the two types of strips for spans l

x

and l

y

separately.

The maximum positive and negative moments per unit width in a slab are determined from

2

x x x

M wl





(1)

2

y y x

M wl





(2)

where

x



and

y



are coefficients given in Table 26 of IS 456, Annex D, cl. D-1.1. Total

design load per unit area is w and lengths of shorter and longer spans are represented by l

x

and

l

y

, respectively. The values of

x



and

y



, given in Table 26 of IS 456, are for nine types of

panels having eight aspect ratios of l

y

/l

x

from one to two at an interval of 0.1. The above

maximum bending moments are applicable only to the middle strips and no redistribution

shall be made.

Tension reinforcing bars for the positive and negative maximum moments are to be provided

in the respective middle strips in each direction. Figure 2.3 shows the positive and negative

coefficients

x



and

y



.

The edge strips will have reinforcing bars parallel to that edge following the minimum

amount as stipulated in IS 456.

(ii) Simply supported slabs

The maximum moments per unit width of simply supported slabs, not having adequate

provision to resist torsion at corners and to prevent the corners from lifting, are determined

from Eqs.(1) and (2), where

x



and

y



are the respective coefficients of moments as given in

Table 27 of IS 456, cl. D-2. The notations M

x

, M

y

, w, l

x

and l

y

are the same as mentioned

below Eqs.(1) and (2) in (i) above.

Detailing of Reinforcement

The detailings of reinforcing bars for (i) restrained slabs and (ii) simply supported slabs are

discussed separately for the bars either for the maximum positive or negative bending

moments or to satisfy the requirement of minimum amount of steel.

(i) Restrained slabs

The maximum positive and negative moments per unit width of the slab calculated by

employing Eqs. (1) and (2) are applicable only to the respective middle strips (Fig.2.3). There

shall be no redistribution of these moments. The reinforcing bars so calculated from the

maximum moments are to be placed satisfying the following stipulations of IS 456.

Figure 2.4 (a) Bars along l

x

only

Figure 2.4 (b) Bars along l

y

only

Figure 2.4 Reinforcement of two-way slab (except torsion reinforcement)

Figure 2.4 (c)

Figure 2.4 (d)

Figure 2.4 Reinforcement of two-way slab (except torsion reinforcement)

 Bottom tension reinforcement bars of mid-span in the middle strip shall extent in the

lower part of the slab to within 0.25l of a continuous edge, or 0.15l of a discontinuous

edge (cl. D-1.4 of IS 456). Bars marked as B1, B2, B5 and B6 in Figs.2.4 a and b are

these bars.

 Top tension reinforcement bars over the continuous edges of middle strip shall extend

in the upper part of the slab for a distance of 0.15l from the support, and at least fifty

per cent of these bars shall extend a distance of 0.3l (cl. D-1.5 of IS 456). Bars marked

as T2, T3, T5 and T6 in Figs.8.19.5 a and b are these bars.

 To resist the negative moment at a discontinuous edge depending on the degree of

fixity at the edge of the slab, top tension reinforcement bars equal to fifty per cent of

that provided at mid-span shall extend 0.1l into the span (cl. D-1.6 of IS 456). Bars

marked as T1 and T4 in Figs. 2.4 a and b are these bars.



the requirement of minimum reinforcement. The bottom and top bars of the edge

strips are explained below.

 2.4 a) are parallel to the edge along l

x

for the edge strip for

span l

y

, satisfying the requirement of minimum amount of steel (cl. D-1.7 of IS 456).

 2.4 b) are parallel to the edge along l

y

for the edge strip for

span l

x

, satisfying the requirement of minimum amount of steel (cl. D-1.7 of IS 456).

 2.4a) are parallel to the edge along l

x

for the edge strip for span

l

y

, satisfying the requirement of minimum amount of steel (cl. D-1.7 of IS 456).

p bars T9 and T10 (Fig. 2.4 b) are parallel to the edge along l

y

for the edge strip for

span l

x

, satisfying the requirement of minimum amount of steel (cl. D-1.7 of IS 456).

(ii) Simply supported slabs

Figure 2.5 Simply supported two-way slab, corners not held down

Figures 2.5 a, b and c present the detailing of reinforcing bars of simply supported slabs not

having adequate provision to resist torsion at corners and to prevent corners from lifting.

Clause D-2.1 stipulates that fifty per cent of the tension reinforcement provided at mid-span

should extend to the supports. The remaining fifty per cent should extend to within 0.1l

x

or

0.1l

y

of the support, as appropriate.

Numerical Problem

Design a R.C. slab for a room measuring 5mx6m size. The slab is simply supported on all the

four edges, with corners held down and carries a super-imposed load of 3 KN/m

2

inclusive of

floor finish etc. Use M20 grade of concrete and Fe 415 grade of steel.

Solution

Computation of loading and bending moment

From deflection point of view l/d=20 for simply supported slab. Let us assume p

t

= 0.2% for

an under-reinforced section. Hence from figure 4 of IS 456:2000, we get modification factor

=1.68.

Hence l/d=20x1.68 =33.6

and d =l/33.6 = 5000/33.6 =148.8 mm

Providing 20 mm nomonal cover and 8 mm bar

D=148.8+20+8 =172.8 mm

Hence assume an overall depth of 180 mm for the purpose of computing dead load

(i) Self weight of slab per m

2

= 0.18x1x1x25 =4.5 KN/m

2

(ii) Super-imposed load @ 3 KN/m

2

= 3 KN/m

2

Total load w =7.5 KN/m

2

Hence w

u

=1.5x7.5 = 11.25 KN/m

2

Taking an effective depth of 150 mm.

Effective l

y

= 6+0.15 = 6.15m

Effective l

x

= 5+0.15 = 5.15m

Therefore

6.15

1.2 2

5.15

y

x

l

  

From table 27 of IS 456:2000

0.072 0.056

xy

and





22

0.072 11.25 5.15 21.483

ux x u x

M w l x x KN m



   

22

0.056 11.25 5.15 16.709

uy y u x

M w l x x KN m



   

For short span, width of middle strip =

33

6.15 4.61

44

y

l x m

Width of edge strip = 0.5x(6.15-4.61) = 0.77m

For long span, width of middle strip =

33

5.15 3.87

44

x

l x m

Width of edge strip = 0.5x(5.15-3.87) = 0.64m

Computation of effective depth and total depth

6

3

21.483 10

88.2

2.761 10

ux

u

M

x

d mm

Rb

x

  

However, from the requirement of deflection keep D= 180 mm.

Therefore , d=180-20-4=156 mm and that for long span d=156-8=148 mm

Computation of steel reinforcement for short span

2

4.6

0.5 1 1 403.2

ck ux

stx

y

ck

fM

A bd mm

f

f bd



   





Spacing of 8 mm bar

1000 50.3

124.7

403.2

x

S mm

However, use 8 mm bars @120 mm c/c for the middle strip of width 4.61m.

Edge strip of length = 0.77m

The reinforcement in the edge strip =

2

0.12 180 1000

216

100

xx

mm

Provide spacing 8 mm 225 c/c.

Computation of steel reinforcement for long span

2

327.9

sty

A mm

Spacing of 8 mm bar

153.4

y

S mm

Provide 8 mm bars @150 mm c/c for the middle strip of width 3.87m.

For edge strip of width = 0.64m ,

st

A

=

2

216mm

Hence provide spacing 8 mm @ 225 c/c.

Torsional reinforcement at corners

Size of torsion mesh =

5.15

1.03

55

x

l

m

from the centre of support or 1.03+0.08 = 1.10

from the edge of the slab.

Area of torsional reinforcement =

2

33

403.2 302.4

44

stx

A x mm

Required spacing 8 mm @ 166 mm

Provide spacing 8 mm @ 150 c/c.

Doubly Reinforced Beam

Figure 2.6 Doubly reinforced beam

Concrete has very good compressive strength and almost negligible tensile strength. Hence,

steel reinforcement is used on the tensile side of concrete. Thus, singly reinforced beams

reinforced on the tensile face are good both in compression and tension. However, these

beams have their respective limiting moments of resistance with specified width, depth and

grades of concrete and steel. The amount of steel reinforcement needed is known as A

st,lim

.

Problem will arise, therefore, if such a section is subjected to bending moment greater than its

limiting moment of resistance as a singly reinforced section.

There are two ways to solve the problem. First, we may increase the depth of the beam,

which may not be feasible in many situations. In those cases, it is possible to increase both

the compressive and tensile forces of the beam by providing steel reinforcement in

compression face and additional reinforcement in tension face of the beam without increasing

the depth (Fig. 2.6). The total compressive force of such beams comprises (i) force due to

concrete in compression and (ii) force due to steel in compression. The tensile force also has

two components: (i) the first provided by A

st

,

lim

which is equal to the compressive force of

concrete in compression. The second part is due to the additional steel in tension - its force

will be equal to the compressive force of steel in compression. Such reinforced concrete

beams having steel reinforcement both on tensile and compressive faces are known as doubly

reinforced beams.

Doubly reinforced beams, therefore, have moment of resistance more than the singly

reinforced beams of the same depth for particular grades of steel and concrete. In many

practical situations, architectural or functional requirements may restrict the overall depth of

the beams. However, other than in doubly reinforced beams compression steel reinforcement

is provided when:

(i) Some sections of a continuous beam with moving loads undergo change of sign of

the bending moment which makes compression zone as tension zone or vice versa.

(ii) The ductility requirement has to be followed.

(iii) The reduction of long term deflection is needed.

Basic Principle

Figure 2.7 Stress, strain and force diagrams of doubly reinforced beam

The moment of resistance M

u

of the doubly reinforced beam consists of (i) M

u,lim

of singly

reinforced beam and (ii) M

u2

because of equal and opposite compression and tension forces

(C

2

and T

2

) due to additional steel reinforcement on compression and tension faces of the

beam (Figs. 2.6 and 7). Thus, the moment of resistance M

u

of a doubly reinforced beam is

Mu = M

u,lim

+ M

u2

(3)

,max ,max

2

,lim

0.36 1 0.42

uu

u ck

xx

M f bd

dd









(4)

Also, M

u

,

lim

can be written

,lim ,lim ,max

0.87 ( 0.416 )

u st y u

M A f d x

(5)

The additional moment M

u2

can be expressed in two ways (Fig. 2.7): considering (i) the

compressive force C

2

due to compression steel and (ii) the tensile force T

2

due to additional

steel on tension face. In both the equations, the lever arm is (d - d'). Thus, we have

( )( )

u sc sc cc

M A f f d d



  

(6)

(0.87 )( )

u st y

M A f d d





(7)

where A

sc

= area of compression steel reinforcement

f

sc

= stress in compression steel reinforcement

f

cc

= compressive stress in concrete at the level of centroid of compression steel reinforcement

A

st2

= area of additional steel reinforcement

Since the additional compressive force C

2

is equal to the additional tensile force T

2

, we have

A

sc

(f

sc

- f

cc

) = A

st2

(0.87 f

y

) (8)

Any two of the three equations (Eqs. 6 - 8) can be employed to determine A

sc

and A

st2

.

The total tensile reinforcement A

st

is then obtained from:

12st st st

A A A

(9)

,lim

1 ,lim

,max

100 0.87 ( 0.42 )

u

st t

yu

M

bd

Ap

f d x





(10)

Determination of f

sc

and f

cc

It is seen that the values of f

sc

and f

cc

should be known before calculating A

sc

. The following

procedure may be followed to determine the value of f

sc

and f

cc

for the design type of

problems (and not for analysing a given section). For the design problem the depth of the

neutral axis may be taken as x

u,max

as shown in Fig. 2.7. From Fig. 2.7, the strain at the level



sc

may be written as

,max

0.0035 1

sc

u

d

x













(11)

f

sc

for Cold worked bars Fe 415 and Fe 500

Table 2.1 Values of f

sc



sc

Stress level

Fe 415

Fe 500

Strain ε

sc

Stress f

sc

(N/mm

2

)

Strain ε

sc

Stress f

sc

(N/mm

2

)

0.80 f

yd

0.00144

288.7

0.00174

347.8

0.85 f

yd

0.00163

306.7

0.00195

369.6

0.90 f

yd

0.00192

324.8

0.00226

391.3

0.95 f

yd

0.00241

342.8

0.00277

413.0

0.975 f

yd

0.00276

351.8

0.00312

423.9

1.0 f

yd

0.00380

360.9

0.00417

434.8

Design type of problems

In the design type of problems, the given data are b, d, D, grades of concrete and steel. The

designer has to determine A

sc

and A

st

of the beam from the given factored moment.

Step 1: To determine M

u, lim

and A

st, lim

from Eqs. 4 and 10, respectively.

Step 2: To determine M

u2

, A

sc

, A

st2

and A

st

from Eqs. 3, 5, 8 and 9, respectively.

Step 3: To select the number and diameter of bars from known values of A

sc

and A

st

.

Analysis type of problems

In the analysis type of problems, the data given are b, d, d', D, f

ck

, f

y

, A

sc

and A

st

. It is required

to determine the moment of resistance M

u

of such beams.

Step 1: To check if the beam is under-reinforced or over-reinforced.

First, x

u,max

is determined assuming it has reached limiting stage using

,maxu

x

d

coefficients as

             

st

is computed from

,max

()

cu

st

u

dx

x









st

has reached the yield strain of steel:

0.002

1.15

y

stat yield

f

E





The beam is under-reinforced or over-

st

is less than or more than the yield strain.

Step 2: To determine M

u,lim

from Eq. 4 and A

st,lim

from the p

t, lim .

Step 3: To determine A

st2

and A

sc

from Eqs. 9 and 8, respectively.

Step 4: To determine M

u2

and M

u

from Eqs. 6 and 3, respectively.

Numerical Problem

Determine the moment of resistance of an existing beam having the following data: b=350

mm; d=900mm;

d



=50mm. Tension reinforcement: 5-20mm HYSD bars (Fe 415);

compression reinforcement 2-20 HYSD bars (Fe 415); grade of concrete M15.

Solution

22

5 (20) 1570.8 ;

4

st

A x mm





22

2 (20) 628.3

4

sc

A x mm





0.87 0.87 415 1570.8 567120

y st

T f A x x N  

0.36 0.446

u ck u sc sc ck sc

C f x b f A f A  

=

1890 628.3 4203

u sc

xf

Let assume

u

x

=230mm; hence

3

7

u

x

=98.6mm >

d



0.0035( )

0.0035(230 50)

0.00274

230

u

sc

u

xd

x







  

Hence from stress-strain curve, we get f

sc

=351 N/mm

2

C

u

= 1890x230 + (628.3x351)-4203=651030 N

This is much more than T

u

= 567120 N. Hence take x

u

= 190 mm.

0.0035( )

0.0035(190 50)

0.00258

190

u

sc

u

xd

x







  

Hence f

sc

=347 N/mm

2

Cu=572919 N T

Therefore, M

u

= 1890x190x(900-0.416x190) + (628.3x347-4203)x(900-50)

476.5 KN-m

Tbeams and Lbeams

Beams having effectively T-sections and L-sections (called T-beams and L-beams) are

commonly encountered in beam-supported slab floor systems [Figs. 2.8]. In such situations, a

portion of the slab acts integrally with the beam and bends in the longitudinal direction of the

beam. This slab portion is called the flange of the T- or L-beam. The beam portion below the

flange is often termed the web, although, technically, the web is the full rectangular portion of

the beam other than the overhanging parts of the flange. Indeed, in shear calculations, the

web is interpreted in this manner.

When the flange is relatively wide, the flexural compressive stress is not uniform over its

width. The stress varies from a maximum in the web region to progressively lower values at

points farther away from the web. In order to operate within the framework of the theory of

flexure, which assumes a uniform stress distribution across the width of the section, it is

necessary to define a reduced effective flange.

            

resists in-plane compressive stresses of uniform magnitude equal to the peak stress in the

original wide flange, such that the value of the resultant longitudinal compressive force is the

same (Fig. 2.8).

Figure 2.8 T-beams and L-beams in beam-supported floor slab systems

The effective flange width is found to increase with increased span, increased web width and

increased flange thickness. It also depends on the type of loading (concentrated, distributed,

etc.) and the support conditions (simply supported, continuous, etc.). Approximate formulae

b

f

(Cl. 23.1.2 of Code) are given as follows:

0

/ 6 6

/12 3

wf

f

wf

l b D forT Beam

b

l b D for L Beam

  









  





(12)

where b

w

is the breadth of the web, D

f

is the thickness of the flange [Fig 2.8], and l

0

is the



the effective span in continuous beams and frames). Obviously, b

f

cannot extend beyond the

slab portion tributary to a beam, i.e., the actual width of slab available. Hence, the calculated

b

f

should be restricted to a value that does not exceed (s

1

+s

2

)/2 

s

1

/2 + b

w

s

1

and s

2

of the slab are as marked in Fig.

2.8.

In some situations, isolated         



the Code [Cl. 23.1.2(c)] recommends the use of the following formula to estimate the

b

f

:

0

/4

0.5

/4

w

f

w

l

b for isolatedT Beams

lb

b

l

b for isolated L Beam

lb

























(13)

where b denotes the actual width of flange; evidently, the calculated value of b

f

should not

exceed b.

Analysis of Singly Reinforced Flanged Sections

The procedure for analysing flanged beams at ultimate loads depends on whether the neutral

axis is located in the flange region [Fig. 2.8(a)] or in the web region [Fig. 2.8(b)].

If the neutral axis lies within the flange (i.e., x

u

D

f

), then as in the analysis at service

loads all the concrete on the tension side of the neutral axis is assumed ineffective, and the T-

section may be analysed as a rectangular section of width b

f

and effective depth d [Fig.

2.8(a)]. Accordingly, Eq. (7) and Eq. (9) are applicable with b replaced by b

f

.

If the neutral axis lies in the web region (i.e., x

u

> D

f

), then the compressive stress is carried

by the concrete in the flange and a portion of the web, as shown in Fig. 2.8(b). It is

convenient to consider the contributions to the resultant compressive force C

u

, from the web

portion (b

w

× x

u

) and the flange portion (width b

f

 b

w

) separately, and to sum up these effects.

Estimating the compressive force C

uw

M

uw

is easy,

as the full stress block is operative:

0.361

uw ck w u

C f b x

(14)

( 0.416 )

uw uw u

M C d x

(15)

Figure 2.9 Behaviour of flanged beam section at ultimate limit state

However, estimating the compressive force C

uf

in the flange is rendered difficult by the fact

that the stress block for the flange portions may comprise a rectangular area plus a truncated

parabolic area [Fig. 2.8(b)]. A general expression for the total area of the stress block

operative in the flange, as well as an expression for the centroidal location of the stress block,

is evidently not convenient to derive for such a case. However, when the stress block over the

flange depth contains only a rectangular area (having a uniform stress 0.447 f

ck

), which

occurs when

3

7

uf

xD

, an expression for C

uf

and its moment contribution M

uf

can easily be

formulated. For the case,

1 / 7/ 3

uf

xD

, an equivalent rectangular stress block (of area

0.447f

ck

y

f

) can be conceived, for convenience, with an equivalent depth y

f

D

f

, as shown in

Fig. 2.8(c). The expression for y

f

          

approximation, because it cannot satisfy the two 

of stress block as well as centroidal location. A general expression for y

f

may be specified for

any x

u

> D

f

:

0.15 0.65 1 / 7 / 3

7 /3

u f u f

f

ff

x D for x D

y

D for D

  















(16)

The expressions for C

uf

and M

uf

are accordingly obtained as:

0.447 ( )

uf ck f w f u f

C f b b y for x D  

(17)

( / 2)

uf uf f

M C d y

(17a)

The location of the neutral axis is fixed by the force equilibrium condition (with y

f

expressed

in terms of x

u

[Eq. 17]).

uf uf st st

C C f A

(18)

where f

st

= 0.87 f

y

for x

u

x

u,max

. Where x

u

> x

u,max

, the strain compatibility method has to be

employed to determine x

u

.

Substituting Eq. 14 and Eq. 17 in Eq. 18, and solving for x

u

,

0.447 ( )

0.361

st st ck f w f

u u f

ck w

f A f b b y

x for x D

fb





(19)

The final expression for the ultimate moment of resistance M

uR

is obtained as:

uR uw uf

M M M

(20)

0.361 ( 0.416 ) 0.447 ( ) ( / 2)

uR ck w u u ck f w f f

M f b x d x f b b y d y     

(21)

Limiting Moment of Resistance

The limiting moment of resistance M

u,lim

is obtained for the condition x

u

= x

u,max

, where x

u,max

takes the values of 0.531d, 0.479d and 0.456d for Fe 250, Fe 415 and Fe 500 grades of tensile

steel reinforcement. The condition x

u

/D

f

       

works out, for x

u

= x

u,max

, as

0.479 / 7 /3

f

dD

, i.e., Ddf    

suggests a simplified condition of

/ 0.2

f

dD

for all grades of steel  to represent the

condition x

u

/D

f



Eq. (21) and Eq. (16) take the following forms:

,lim ,max ,max

,max

0.361 ( 0.416 )

0.447 ( ) ( / 2) for

u ck w u u

ck f w f f u f

M f b x d x

f b b y d y x D



   

(22)

,max

0.15 0.65 / 0.2

/ 0.2

u f f

f

ff

x D for D d

y

D for D d

















(23)

The advantage of using Eq. (23) in lieu of the more exact Eq. (16) (with x

u

= x

u,max

) is that the

estimation of y

f

is made somewhat simpler. Of course, for x

u,max

D

f

(i.e., neutral axis within

the flange),

,lim ,max ,max ,max

0.361 ( 0.416 )

u ck f u u u f

M f b x d x for x D  

(24)

As mentioned earlier, when it is found by analysis of a given T-section that x

u

> x

u,max

, then

the strain compatibility method has to be applied. As an approximate and conservative

estimate, M

uR

may be taken as M

u,lim

, given by Eq. (23) / (24). From the point of view of

design (to be discussed in Chapter 5), M

u,lim

provides a measure of the ultimate moment

capacity that can be expected from a T-section of given proportions. If the section has to be

designed for a factored moment M

u

> M

u,lim

, then this calls for the provision of compression

reinforcement in addition to extra tension reinforcement.

Design Procedure

In the case of a continuous flanged beam, the negative moment at the face of the support

generally exceeds the maximum positive moment (at or near the midspan), and hence governs

the proportioning of the beam cross-section. In such cases of negative moment, if the slab is

located on top of the beam (as is usually the case), the flange is under flexural tension and

hence the concrete in the flange is rendered ineffective. The beam section at the support is

therefore to be designed as a rectangular section for the factored negative moment. Towards

the midspan of the beam, however, the beam behaves as a proper flanged beam (with the

flange under flexural compression). As the width of the web b

w

and the overall depth D are

already fixed from design considerations at the support, all that remains to be determined is

the area of reinforcing steel; the effective width of flange is determined as suggested by the

Code .

The determination of the actual reinforcement in a flanged beam depends on the location of

the neutral axis x

u

, which, of course, should be limited to x

u,max

. If M

u

exceeds M

u,lim

for a

singly reinforced flange section, the depth of the section should be suitably increased;

otherwise, a doubly reinforced section is to be designed.

Neutral Axis within Flange (x

u

D

f

):

This is, by far, the most common situation encountered in building design. Because of the

very large compressive concrete area contributed by the flange in T-beam and L-beams of

usual proportions, the neutral axis lies within the flange (x

u

 D

f

), whereby the section

behaves like a rectangular section having width b

f

and effective depth d.

A simple way of first checking x

u

D

f

is by verifying

()

uf

u uR x D

MM





where

()

uf

uR x D

M



is the limiting ultimate moment of resistance for the condition

uf

xD

and is given by

( ) 0.361 ( 0.416 )

uf

uR x D ck f f f

M f b D d D





(25)

It may be noted that the above equation is meaning only if

,maxuf

xD

. In rare situations

involving very thick flanges and relatively shallow beams,

,maxu

x

may be less than D

f

. in such

cases, M

u,lim

is obtained by substituting x

u,max

in place of D

f

in Eq. (25).

Neutral Axis within Web (x

u

> D

f

):

When

()

uf

u uR x D

MM





, it follows that

uf

xD

. The accurate determination of

u

x

can be

laborious. The contributions of the compressive forces

uw

C

and

uf

C



may be accounted for separately as follows:

( 0.416 ) ( / 2)

uR uw u uf f

M C d x C d y   

(26)

0.361

uw ck w u

C f b x

(27)

0.447 ( )

uf ck f w f

C f b b y

(28)

and the equivalent flange thickness y

f

is equal to or less than D

f

depending on whether x

u

exceeds 7D

f

/3 or not.

For x

u,max

 D

f

/3, the value of the ultimate moment of resistance

7 /3

()

uf

uR x D

M



corresponding to

7 / 3

uf

xD

and

ff

yD

may be first computed. If the factored moment

7 /3

()

uf

u uR x D

MM





, it follows that

7 /3

uf

xD

and

ff

yD

. Otherwise,

7 /3

f u f

D x D

for

7 /3

( ) ( )

u f u f

uR x D u uR x D

M M M





and

0.15 0.65

f u f

y x D

(29)

Inserting the appropriate value  Df or the expression for y

f

in Eq. (29), in Eq. (26), the

resulting quadratic equation (in terms of the unknown x

u

) can be solved to yield the correct

value of x

u.

. Corresponding to this value of x

u,

the values of C

uw

and C

uf

can be computed [Eq.

(27), (28)] and the required A

st

obtained by solving the force equilibrium equation.

0.87

u f st uw uf

T f A C C  

()

0.87

uw uf

st required

y

CC

A

f





(30)

Numerical Problem

A continuous T-beam has the cross-sectional dimensions shown in figure below. The web

dimensions have been determined from the consideration of negative moment at support and

shear strength requirements. The span is 10 m and the design moment at midspan under

factored loads is 800 kNm. Determine the flexural reinforcement requirement at midspan.

Consider Fe 415 steel. Assume that the beam is subjected to moderate exposure conditions.

Solution

Determining approximate A

st

Effective flange width b

f

Actual flange width provided =1500mm; D

f

=100 mm; b

w

=300mm

Maximum width permitted =(0.7x10000)/6 + 300 + (6x100) =2067 mm >1500 mm

Therefore, b

f

=1500 mm

Assuming d=650 mm and a lever arm z equal to larger of 0.9d = 585 mm

And d- Df/2 = 600mm i.e. z=600 mm

6

2

800 10

( ) 3693

0.87 415 600

st required

x

A mm

xx



Figure: Reinforcement of T-beam of Example Problem

Determining actual Ast

x

u,max

= 0.479 × 618 =296 mm

As x

u,max

>D

f

=100mm, the condition x

u

=D

f

satisfies

,maxuu

xx

f

ck

= 25 MPa

()

uf

uR x D

M



0.362 × 25 × 1500 × 100 × (618  0.416 × 100)

= 782.5 × 10

6

Nmm < M

u

= 800 kNm

⇒ x

u

> D

f

and M

u

= C

uw

(d  0.416 x

u

) + C

uf

(d  y

f

/2)

where C

uw

= 0.362f

ck

b

w u

= 0.362 × 25 × 300x

u

= (2715x

u

) N

and C

uf

= 0.447f

ck

(b

f

 b

w

)y

f

= 0.447 × 25 × (1500  300)y

f

= (13410y

f

)

Considering x

u

= 7D

f

/3 = 233 mm ( < x

u,max

= 296 mm), y

f

= D

f

= 100 mm

⇒

7 /3

()

uf

uR x D

M



(2715 × 233)(618  0.416 × 233) + (13410x100)x(618-100/2)

=1091.3x10

6

Nmm >M

u

= 800 KNm



Evidently,

7

3

f u f

D x D

, for which y

f

=0.15x

u

+o.65D

f

C

uf

= 13410(0.15x.65 × 100) = (2011.5x

u

+ 871650) N

M

u

= 800 × 10

6

= (2715x

u

)(618  0.416x

u

)

+ (2011.5xu+871650)x[618-(0.15xu+65)/2]

= -1280.3x

u

2

+ 2790229.5 x

u

+ 510.35×106

Solving this quadratic equation,

x

u

= 109.3 mm < x

u,max

= 296 m

⇒ y

f

= 0.15x

u

+ 65 = 81.4 mm

Applying T

u

= 0.87f

y

A

st

= C

uw

+C

uf

2

(2715 109.3) (13410 81.4)

( ) 3845

0.87 415

st required

xx

A mm

x





The reinforcement (5- 

st

=4020 mm

2

, based on appropriate estimate of A

st

[Fig.] is

evidently adequate and appropriate.

Design of Staircase

The staircase is an important component of a building, and often the only means of access

between the various floors in the building. It consists of a flight of steps, usually with one or

more intermediate landings (horizontal slab platforms) provided between the floor levels. The

horizontal top portion of a step (where the foot rests) is termed tread and the vertical

projection of the step (i.e., the vertical distance between two neighbouring steps) is called

riser [Fig. 2.10]. Values of 300 mm and 150 mm are ideally assigned to the tread and riser

respectively  particularly in public buildings. However, lower values of tread (up to 250

mm) combined with higher values of riser (up to 190 mm) are resorted to in residential and

factory buildings. The width of the stair is generally around 1.1  1.6m, and in any case,

should normally not be less than 850 mm; large stair widths are encountered in entrances to

public buildings. The horizontal projection (plan) of an inclined flight of steps, between the

first and last risers, is termed going. A typical flight of steps consists of two landings and one

going, as depicted in Fig. 2.10(a). Generally, risers in a flight should not exceed about 12 in

number. The steps in the flight can be designed in a number of ways: with waist slab, with

tread-riser arrangement (without waist slab) or with isolated tread slabs  as shown in Fig.

2.10(b), (c), (d) respectively.

Figure 2.10 A typical flight in a staircase

TYPES OF STAIRCASES

Geometrical Configurations

A wide variety of staircases are met with in practice. Some of the more common geometrical

configurations are depicted in Fig. 2.11. These include:

2.11 (a)]

-turn stairs [Fig. 2.11 (b)]

-legged stairs [Fig. 2.11 (c)]

2.11 (d)]

2.11 (e)]

2.11 (f)]

Fig. 2.11 Common geometrical configurations of stairs

Structural Classification

Structurally, staircases may be classified largely into two categories, depending on the

predominant direction in which the slab component of the stair undergoes flexure:

1. Stair slab spanning transversely (stair widthwise);

2. Stair slab spanning longitudinally (along the incline).

Stair Slab Spanning Transversely

The slab component of the stair (whether comprising an isolated tread slab, a tread-riser unit

or a waist slab) is supported on its side(s) or cantilevers laterally from a central support. The

slab supports gravity loads by bending essentially in a transverse vertical plane, with the

span along the width of the stair.

In the case of the cantilevered slabs, it is economical to provide isolated treads (without

risers). However, the tread-riser type of arrangement and the waist slab type are also

sometimes employed in practice, as cantilevers. The spandrel beam is subjected to torsion



When the slab is supported at the two sides by means , it

may be designed as simply supported, but reinforcement at the top should be provided near

   

fixity.

Stair Slab Spanning Longitudinally

In this case, the supports to the stair slab are provided parallel to the riser at two or more

locations, causing the slab to bend longitudinally between the supports. It may be noted that

longitudinal bending can occur in configurations other than the straight stair configuration,

such as quarter-turn stairs, dog-legged stairs, open well stairs and helicoidal stairs .

          -

type. The slab thickness depe-

to-centre distance between the beam/wall supports, according to the Code (Cl. 33.1a, c).In

certain situations, beam or wall supports may not be available parallel to the riser at the

landing. Instead, the flight is supported between the landings, which span transversely,

parallel to the risers. In such cases, the Code(Cl. 33.1b) specifies that the effective span for

the flight (spanning longitudinally) should be taken as the going of the stairs plus at each end

either half the width of the landing or one metre, whichever is smaller.

Numerical Problem

-legged staircase for an office building, given the following

data:



0 mm, tread = 270 mm;





2

inishes load = 0.6 kN/m

2

Assume the stairs to be supported on 230 mm thick masonry walls at the outer edges of the

landing, parallel to the risers [Fig. 12.13(a)]. Use M 20 concrete and Fe 415 steel. Assume

mild exposure conditions.

Solution

Given: R = 160 mm, T = 270 mm ⇒+RT22

= 314 mm Effective span = c/c distance between supports = 5.16 m [Fig below].

l20 = 5160/20 = 258 260 mm.

Assuming 20 mm clear cover (mild 

effective depth d = 260  20  12/2 = 234 mm.

The slab thickness in the landing regions may be taken as 200 mm, as the bending

moments are relatively low here.

Loads on going [fig. below] on projected plan area:

(1) self-weight of waist slab @ 25 × 0.26 × 314/270 = 7.56 kN/m

2

(2) self-weight of steps @ 25 × (0.5x0.16) = 2.00 kN/m

2

(3) finishes (given) = 0.60 kN/m

2

(4) live load (given) = 5.00 kN/m

2

Total =15.16 kN/m

2

⇒Factored load = 15.16 × 1.5 = 22.74 kN/m

2

Loads on landing

(1) self-weight of slab @ 25 × 0.20 = 5.00 kN/m

2

(2) finishes @ 0.6 kN/m

2

(3) live loads @ 5.0 kN/m

2

Total =10.60 kN/m

2

⇒Factored load = 10.60 × 1.5 = 15.90 kN/m

2

Design Moment [Fig. below]

Reaction R= (15.90x1.365)+(22.74x2.43)/2 = 49.33 kN/m

Maximum moment at midspan:

M

u

= (49.33 × 2.58)  (15.90 × 1.365) × (2.58  1.365/2)

 (22.74) × (2.58  1.365)

2

/2

= 69.30 kNm/m

Main reinforcement

2

u

M

R

bd



= 1.265 MPa

Assuming f

ck

= 20 MPa, f

y

= 415 MPa,

2

0.381 10

100 100

t st

pA

x





⇒

2 3 2

( ) (0.381 10 ) 10 234 892 /

st req

A x x x mm m









Provide 16 @ 220c/c

Distributors

2

( ) 0.0012 312 /

st req

A bt mm m

251 mm

Provide 10 @ 250c/c as distributors.

Figure for numerical problem

MODULE-3

Introduction

Compression members are structural elements primarily subjected to axial compressive forces

and hence, their design is guided by considerations of strength and buckling. Examples of

compression member pedestal, column, wall and strut.

Definitions

(a) Effective length: The vertical distance between the points of inflection of the compression

member in the buckled configuration in a plane is termed as effective length l

e

of that

compression member in that plane. The effective length is different from the unsupported

length l of the member, though it depends on the unsupported length and the type of end

restraints. The relation between the effective and unsupported lengths of any compression

member is

l

e

= k l (1)

Where k is the ratio of effective to the unsupported lengths. Clause 25.2 of IS 456 stipulates

the effective lengths of compression members (vide Annex E of IS 456). This parameter is

needed in classifying and designing the compression members.

(b) Pedestal: Pedestal is a vertical compression member whose effective length l

e

does not

exceed three times of its least horizontal dimension b (cl. 26.5.3.1h, Note). The other

horizontal dimension D shall not exceed four times of b.

(c) Column: Column is a vertical compression member whose unsupported length l shall not

exceed sixty times of b (least lateral dimension), if restrained at the two ends. Further, its

unsupported length of a cantilever column shall not exceed 100b

2

/D, where D is the larger

lateral dimension which is also restricted up to four times of b (vide cl. 25.3 of IS 456).

(d) Wall: Wall is a vertical compression member whose effective height H

we

to thickness t (least

lateral dimension) shall not exceed 30 (cl. 32.2.3 of IS 456). The larger horizontal dimension i.e.,

the length of the wall L is more than 4t.

Classification of Columns Based on Types of Reinforcement

Figure 3.1(a) Tied Column

Figure 3.1(b) Column with helical reinforcement

Figure 3.1(c) Composite column (steel section)

Figure 3.1(d) Composite column (steel pipe)

Figure 3.1 Tied, helically bound and composite columns

Based on the types of reinforcement, the reinforced concrete columns are classified into three

groups:

(i) Tied columns: The main longitudinal reinforcement bars are enclosed within closely

spaced lateral ties (Fig.3.1a).

(ii) Columns with helical reinforcement: The main longitudinal reinforcement bars are

enclosed within closely spaced and continuously wound spiral reinforcement. Circular and

octagonal columns are mostly of this type (Fig. 3.1b).

(iii) Composite columns: The main longitudinal reinforcement of the composite columns

consists of structural steel sections or pipes with or without longitudinal bars (Fig. 3.1c and

d).

Out of the three types of columns, the tied columns are mostly common with different shapes

of the cross-sections viz. square, rectangular etc. Helically bound columns are also used for

circular or octagonal shapes of cross-sections.

Classification of Columns Based on Loadings

Figure 3.2(a) Axial loading (concentric) Figure 3.2(b) Axial loading with uniaxial bending

Figure 3.2(c) Axial loading with biaxial bending

Columns are classified into the three following types based on the loadings:

(i) Columns subjected to axial loads only (concentric), as shown in Fig. 3.2a.

(ii) Columns subjected to combined axial load and uniaxial bending, as shown in Fig. 3.2b.

(iii) Columns subjected to combined axial load and bi-axial bending, as shown in Fig. 3.2c.

Classification of Columns Based on Slenderness Ratios

Columns are classified into the following two types based on the slenderness ratios:

(i) Short columns

(ii) Slender or long columns

Figure 3.3 Modes of failure of columns

Figure 3.3 presents the three modes of failure of columns with different slenderness ratios

when loaded axially. In the mode 1, column does not undergo any lateral deformation and

collapses due to material failure. This is known as compression failure. Due to the combined

effects of axial load and moment a short column may have material failure of mode 2. On the

other hand, a slender column subjected to axial load only undergoes deflection due to beam-

column effect and may have material failure under the combined action of direct load and

bending moment. Such failure is called combined compression and bending failure of mode

2. Mode 3 failure is by elastic instability of very long column even under small load much

before the material reaches the yield stresses. This type of failure is known as elastic

buckling.

The slenderness ratio of steel column is the ratio of its effective length l

e

to its least radius of

gyration r. In case of reinforced concrete column, however, IS 456 stipulates the slenderness

ratio as the ratio of its effective length l

e

to its least lateral dimension. As mentioned earlier in

sec. 3.1(a), the effective length l

e

is different from the unsupported length, the rectangular

reinforced concrete column of cross-sectional dimensions b and D shall have two effective

lengths in the two directions of b and D. Accordingly, the column may have the possibility of

buckling depending on the two values of slenderness ratios as given below:

Slenderness ratio about the major axis = l

ex

/D

Slenderness ratio about the minor axis = l

ey

/b

Based on the discussion above, cl. 25.1.2 of IS 456 stipulates the following:

A compression member may be considered as short when both the slenderness ratios l

ex

/D

and l

ey

/b are less than 12 where l

ex

= effective length in respect of the major axis, D = depth in

respect of the major axis, l

ey

= effective length in respect of the minor axis, and b = width of

the member. It shall otherwise be considered as a slender compression member.

Further, it is essential to avoid the mode 3 type of failure of columns so that all columns

should have material failure (modes 1 and 2) only. Accordingly, cl. 25.3.1 of IS 456

stipulates the maximum unsupported length between two restraints of a column to sixty times

its least lateral dimension. For cantilever columns, when one end of the column is

unrestrained, the unsupported length is restricted to 100b

2

/D where b and D are as defined

earlier.

Longitudinal Reinforcement

The longitudinal reinforcing bars carry the compressive loads along with the concrete. Clause

26.5.3.1 stipulates the guidelines regarding the minimum and maximum amount, number of

bars, minimum diameter of bars, spacing of bars etc. The following are the salient points:

(a) The minimum amount of steel should be at least 0.8 per cent of the gross cross-sectional

area of the column required if for any reason the provided area is more than the required area.

(b) The maximum amount of steel should be 4 per cent of the gross cross-sectional area of the

column so that it does not exceed 6 per cent when bars from column below have to be lapped

with those in the column under consideration.

(c) Four and six are the minimum number of longitudinal bars in rectangular and circular

columns, respectively.

(d) The diameter of the longitudinal bars should be at least 12 mm.

(e) Columns having helical reinforcement shall have at least six longitudinal bars within and

in contact with the helical reinforcement. The bars shall be placed equidistant around its inner

circumference.

(f) The bars shall be spaced not exceeding 300 mm along the periphery of the column.

(g) The amount of reinforcement for pedestal shall be at least 0.15 per cent of the cross-

sectional area provided.

Transverse Reinforcement

Transverse reinforcing bars are provided in forms of circular rings, polygonal links (lateral

ties) with internal angles not exceeding 135

o

or helical reinforcement. The transverse

reinforcing bars are provided to ensure that every longitudinal bar nearest to the compression

face has effective lateral support against buckling. Clause 26.5.3.2 stipulates the guidelines of

the arrangement of transverse reinforcement. The salient points are:

Figure 3.4 Lateral tie (Arrangement 1)

(a) Transverse reinforcement shall only go round corner and alternate bars if the longitudinal

bars are not spaced more than 75 mm on either side (Fig.3.4).

Figure 3.5 Lateral tie (Arrangement 2)

(b) Longitudinal bars spaced at a maximum distance of 48 times the diameter of the tie shall

be tied by single tie and additional open ties for in between longitudinal bars (Fig.3.5).

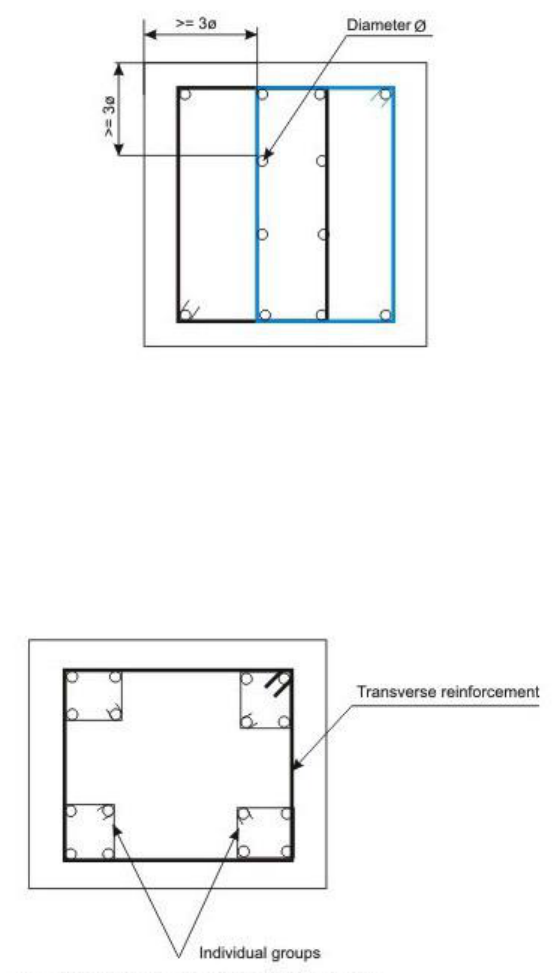
Figure 3.6 Lateral tie (Arrangement 3)

(c) For longitudinal bars placed in more than one row (Fig.10.21.9): (i) transverse

reinforcement is provided for the outer-most row in accordance with (a) above, and (ii) no bar

of the inner row is closer to the nearest compression face than three times the diameter of the

largest bar in the inner row.

Figure 3.7 Lateral tie (Arrangement 4)

(d) For longitudinal bars arranged in a group such that they are not in contact and each group

is adequately tied as per (a), (b) or (c) above, as appropriate, the transverse reinforcement for

the compression member as a whole may be provided assuming that each group is a single

longitudinal bar for determining the pitch and diameter of the transverse reinforcement. The

diameter of such transverse reinforcement should not, however, exceed 20 mm (Fig.3.7).

Pitch and Diameter of Lateral Ties

(a) Pitch: The maximum pitch of transverse reinforcement shall be the least of the following:

(i) the least lateral dimension of the compression members;

(ii) sixteen times the smallest diameter of the longitudinal reinforcement bar to be

tied; and

(iii) 300 mm.

(b) Diameter: The diameter of the polygonal links or lateral ties shall be not less than one-

fourth of the diameter of the largest longitudinal bar, and in no case less than 6 mm.

Assumptions in the Design of Compression Members by Limit State of Collapse

The following are the assumptions in addition to given in 38.1 (a) to (e) for flexure for the

design of compression members (cl. 39.1 of IS 456).

(i) The maximum compressive strain in concrete in axial compression is taken as 0.002.

(ii) The maximum compressive strain at the highly compressed extreme fibre in concrete

subjected to axial compression and bending and when there is no tension on the section shall

be 0.0035 minus 0.75 times the strain at the least compressed extreme fibre.

Minimum Eccentricity

In practical construction, columns are rarely truly concentric. Even a theoretical column

loaded axially will have accidental eccentricity due to inaccuracy in construction or variation

of materials etc. Accordingly, all axially loaded columns should be designed considering the

minimum eccentricity as stipulated in cl. 25.4 of IS 456 and given below (Fig.3.2c)

e

x min 

greater of (l/500 + D/30) or 20 mm

e

y min 

greater of (l/500 + b/30) or 20 mm

where l, D and b are the unsupported length, larger lateral dimension and least lateral

dimension, respectively.

Governing Equation for Short Axially Loaded Tied Columns

Factored concentric load applied on short tied columns is resisted by concrete of area A

c

and

longitudinal steel of areas A

sc

effectively held by lateral ties at intervals. Assuming the design

strengths of concrete and steel are 0.4f

ck

and 0.67f

y

, respectively, we can write

P

u

= 0.4f

ck

A

c

+ 0.67f

y

A

sc

(1)

Where P

u

= factored axial load on the member,

f

ck

= characteristic compressive strength of the concrete,

A

c

= area of concrete,

f

y

= characteristic strength of the compression reinforcement, and

A

sc

= area of longitudinal reinforcement for columns.

The above equation, given in cl. 39.3 of IS 456, has two unknowns Ac and A

sc

to be

determined from one equation. The equation is recast in terms of A

g

, the gross area of

concrete and p, the percentage of compression reinforcement employing

A

sc

= pA

g

/100 (2)

A

c

= A

g

(1  p/100) (3)

Accordingly, we can write

P

u

/A

g

= 0.4f

ck

+ (p/100) (0.67f

y

 0.4f

ck

) (4)

Equation 4 can be used for direct computation of A

g

when P

u

, f

ck

and f

y

are known by

assuming p ranging from 0.8 to 4 as the minimum and maximum percentages of longitudinal

reinforcement. Equation 10.4 also can be employed to determine A

g

and p in a similar manner

by assuming p.

Numerical Problem

Design the reinforcement in a column of size 400 mm x 600 mm subjected to an axial load of

2000 kN under service dead load and live load. The column has an unsupported length of 4.0

m and effectively held in position and restrained against rotation in both ends. Use M 25

concrete and Fe 415 steel.

Solution

Step 1: To check if the column is short or slender

Given l = 4000 mm, b = 400 mm and D = 600 mm. Table 28 of IS 456 = l

ex

= l

ey

= 0.65(l) =

2600 mm. So, we have

l

ex

/D = 2600/600 = 4.33 < 12

l

ey

/b = 2600/400 = 6.5 < 12

Hence, it is a short column.

Step 2: Minimum eccentricity

e

x min

= Greater of (l

ex

/500 + D/30) and 20 mm = 25.2 mm

e

y min

= Greater of (l

ey

/500 + b/30) and 20 mm = 20 mm

0.05 D = 0.05(600) = 30 mm > 25.2 mm (= e

x min

)

0.05 b = 0.05(400) = 20 mm = 20 mm (= e

y min

)

Hence, the equation given in cl.39.3 of IS 456 (Eq.(1)) is applicable for the design here.

Step 3: Area of steel

Fro Eq.10.4, we have

P

u

= 0.4 f

ck

A

c

+ 0.67 f

y

A

sc

3000(10

3

) = 0.4(25){(400)(600)  A

sc

} + 0.67(415) A

sc

which gives,

A

sc

= 2238.39 mm

2

Provide 6-20 mm diameter and 2-16 mm diameter rods giving 2287 mm

2

(> 2238.39 mm

2

)

and p = 0.953 per cent, which is more than minimum percentage of 0.8 and less than

maximum percentage of 4.0. Hence, o.k.

Step 4: Lateral ties

The diameter of transverse reinforcement (lateral ties) is determined from cl.26.5.3.2 C-2 of

                   

longitudinal reinforcement = 20 mm. So, the diameter of bars used as lateral ties = 6 mm.

The pitch of lateral ties, as per cl.26.5.3.2 C-1 of IS 456, should be not more than the least of

(i) the least lateral dimension of the column = 400 mm

(ii) sixteen times the smallest diameter of longitudinal reinforcement bar to be tied =

16(16) = 256 mm

(iii) 300 mm

Reinforcement Detailing

Let us use p = pitch of lateral ties = 250 mm.

IS Code Method for Design of Columns under Axial Load and Biaxial Bending

IS 456 recommends the following simplified method, based on Bresler's formulation, for the

design of biaxially loaded columns. The relationship between M

uxz

and M

uyz

for a particular

value of P

u

= P

uz

, expressed in non-dimensional form is:

11

( / ) ( / ) 1

nn

ux ux uy uy

M M M M





(5)

where M

ux

and M

uy

= moments about x and y axes due to design loads, and

n



is related to P

u

/P

uz

,

where

P

uz

= 0.45 f

ck

A

c

+ 0.75 f

y

A

sc

= 0.45 A

g

+ (0.75 f

y

- 0.45 f

ck

) A

sc

(6)

where A

g

= gross area of the section, and

A

sc

= total area of steel in the section

M

uxz

, M

uyz

, M

ux1

and M

uy1

are explained earlier.

n



= 1.0, when P

u

/P

uz



n



= 0.67 + 1.67 P

u

/P

uz

, when 0.2 < (P

u

/P

uz

) < 0.8 (7)

n



= 2.0, when (P

u

/P

uz

)



0.8

Numerical Problem

Design the reinforcement to be provided in the short column is subjected to P

u

= 2000 kN,

M

ux

= 130 kNm (about the major principal axis) and M

uy

= 120 kNm (about the minor

principal axis). The unsupported length of the column is 3.2 m, width b = 400 mm and depth

D = 500 mm. Use M 25 and Fe 415 for the design.

Solution

Step 1: Verification of the eccentricities

Given: l = 3200 mm, b = 400 mm and D = 500 mm,

The minimum eccentricities are:

e

xmin

= greater of (3200/500 + 400/30) and 20 mm = 19.73 mm or 20 mm = 20 mm

e

ymin

= greater of (3200/500 + 500/30) and 20 mm = 23.07 mm or 20 mm = 23.07 mm

Again from P

u

= 2000 kN, M

ux

= 130 kNm and M

uy

= 120 kNm, we have e

x

= M

ux

/P

u

=

130(10

6

)/2000(10

3

) = 65 mm and e

y

= M

uy

/P

u

= 120(10

6

)/2000(10

3

) = 60 mm. Both e

x

and e

y

are greater than e

xmin

and e

ymin

, respectively.

Step 2: Assuming a trial section including the reinforcement

We have b = 400 mm and D = 500 mm. For the reinforcement,

22

1.15( )

u ux uy

M M M

,

becomes 203.456 kNm. Accordingly,

P

u

/f

ck

bD = 2000(10

3

)/(25)(400)(500) = 0.4

M

u

/f

ck

bD

2

= 203.456(10

6

)/(25)(400)(500)(500) = 0.0814

Assuming d' = 60 mm, we have d'/D = 0.12. From Charts 44 and 45, the value of p/f

ck

is

interpolated as 0.06. Thus, p = 0.06(25) = 1.5 per cent, giving A

sc

= 3000 mm

2

. Provide 12-20

mm diameter bars of area 3769 mm

2

, actual p provided = 1.8845 per cent. So, p/f

ck

= 0.07538.

Step 3: Determination of M

ux1

and M

uy1

We have P

u

/f

ck

bD = 0.4 and p/f

ck

= 0.07538 in step 2. Now, we get M

ux1

/f

ck

bD

2

from chart

corresponding to d' = 58 mm i.e., d'/D = 0.116. We interpolate the values of Charts 44 and

45, and get M

ux1

/f

ck

bD

2

= 0.09044. So, M

ux1

= 0.0944(25)(400)(500(500)(10

-6

) = 226.1 kNm.

For M

ux1

, d'/b = 58/400 = 0.145. In a similar manner, we get M

uy1

=

0.0858(25)(400)(400)(500)(10

-6

) = 171.6 kNm.

As M

ux1

and M

uy1

are significantly greater than M

ux

and M

uy

, respectively, redesign of the

section is not needed.

Step 4: Determination of P

uz

and

n



We have P

uz

= 0.45(25)(400)(500) + {0.75(415) - 0.45(25)}(3769) = 3380.7 kN.

Now, the value of

n



is obtained for P

u

/P

uz

= 2000/3380.7 = 0.5916, i.e., 0.2 < P

u

/P

uz

< 0.8,

which gives, nP

u

/P

uz

) = 1.658.

Step 5: Checking the adequacy of the section

Using the values of M

ux

, M

ux1

, M

uy

, M

uy1

and

n



in Eq.(5), we have (130/226.1)

1.658

+

(120/171.6)

1.658

= 0.9521 < 1.0. Hence, the design is safe.

Step 6: Design of transverse reinforcement

As per cl.26.5.3.2c of IS 456, the diameter of lateral tie should be > (20/4) mm diameter.

Provide 8 mm diameter bars following the arrangement shown in Fig.10.26.4. The spacing of

lateral tie is the least of:

(a) 400 mm = least lateral dimension of column,

(b) 320 mm = sixteen times the diameter of longitudinal reinforcement (20 mm),

(c) 300 mm

Accordingly, provide 8 mm lateral tie alternately @ 250 c/c (Fig.10.26.4).

Reinforcement Detailing

Slender Columns

Columns having both l

ex

/D and l

ey

/b less than twelve are designated as short and otherwise,

they are slender, where l

ex

and l

ey

are the effective lengths with respect to major and minor

axes, respectively; and D and b are the depth and width of rectangular columns, respectively.

Design of Slender Columns

The design of slender compression members shall be based on the forces and the moments

determined from an analysis of the structure, including the effect of deflections on moments

and forces. When the effect of deflections are not taken into account in the analysis,

additional moment given in cl no 39.7.1 of IS 456:2000 shall be taken into account in the

appropriate direction.

The additional moments M, and My, shall be calculated by the following formulae:

M

ax

= (P

u

D/2000) (l

ex

/D)

2

M

ay

= (P

u

b/2000) (l

ey

/b)

2

Where P

u

= axial load on the member,

l

ex

= effective length in respect of the major axis,

l

ey

= effective length in respect of the minor axis,

D = depth of the cross-section at right angles to the major axis, and

b = width of the member.

The values given by equation 39.7.1 may be multiplied by the following factor:

(i) For P

u

> P

ubx

: k

ax

= (P

uz

– P

u

)/(P

uz

– P

ubx

)

(ii) For P

u

> P

uby

: k

ay

= (P

uz

– P

u

)/(P

uz

– P

uby

)

with a condition that k

ax

and k

ay



where P

u

= axial load on compression member

P

uz

= 0.45 f

ck

A

c

+ 0.75 f

y

A

st

P

ubx

, P

uby

= axial loads with respect to major and minor axes, respectively, corresponding to

the condition of maximum compressive strain of 0.0035 in concrete and tensile strain of

0.002 in outermost layer of tension steel.

Numerical Problem

Determine the reinforcement required for a braced column against sidesway with the

following data: size of the column = 350 x 450 mm (Fig.10.27.18); concrete and steel grades

= M 30 and Fe 415, respectively; effective lengths l

ex

and l

ey

= 7.0 and 6.0 m, respectively;

unsupported length l = 8 m; factored load P

u

= 1700 kN; factored moments in the direction of

larger dimension = 70 kNm at top and 30 kNm at bottom; factored moments in the direction

of shorter dimension = 60 kNm at top and 30 kNm at bottom. The column is bent in double

curvature. Reinforcement will be distributed equally on four sides.

Solution

Solution 1:

Step 1: Checking of slenderness ratios

l

ex

/D = 7000/450 = 15.56 > 12,

l

ey

/b = 6000/350 = 17.14 > 12.

Hence, the column is slender with respect to both the axes.

Step 2: Minimum eccentricities and moments due to minimum eccentricities

e

x min

= l/500 + D/30 = 8000/500 + 450/30 = 31.0 > 20 mm

e

y min

= l/500 + b/30 = 8000/500 + 350/30 = 27.67 > 20 mm

M

ox

(Min. ecc.) = P

u

(e

x min

) = (1700) (31) (10

-3

) = 52.7 kNm

M

oy

(Min. ecc.) = P

u

(e

y min

) = (1700) (27.67) (10

-3

) = 47.04 kNm

Step 3: Additional eccentricities and additional moments

Table I of SP-16

For l

ex

/D = 15.56, Table I of SP-16 gives:

e

ax

/D = 0.1214, which gives e

ax

= (0.1214) (450) = 54.63 mm

For l

ey

/D = 17.14, Table I of SP-16 gives:

e

ay

/b = 0.14738, which gives e

ay

= (0.14738) (350) = 51.583 mm

Step 4: Primary moments and primary eccentricities (Eqs.10.88 and 89)

M

ox

= 0.6M

2

 0.4M

1

= 0.6(70)  M

2

(= 28 kNm).

Hence, o.k.

M

oy

= 0.6M

2

 0.4M

1

= 0.6(60)  M

2

(= 24

kNm). Hence, o.k.

Primary eccentricities:

e

x

= M

ox

/P

u

= (30/1700) (10

3

) = 17.65 mm

e

y

= M

oy

/P

u

= (24/1700) (10

3

) = 14.12 mm

Since, both primary eccentricities are less than the respective minimum eccentricities (see

Step 2), the primary moments are revised to those of Step 2. So, M

ox

= 52.7 kNm and M

oy

=

47.04 kNm.

Step 5: Modification factors

To determine the actual modification factors, the percentage of longitudinal reinforcement

should be known. So, either the percentage of longitudinal reinforcement may be assumed or

the modification factor may be assumed which should be verified subsequently. So, we

assume the modification factors of 0.55 in both directions.

Step 6: Total factored moments

M

ux

= M

ox

+ (Modification factor) (M

ax

) = 52.7 + (0.55) (92.548)

= 52.7 + 50.9 = 103.6 kNm

M

uy

= M

oy

+ (Modification factor) (M

ay

) = 47.04 + (0.55) (87.43)

= 47.04 + 48.09 = 95.13 kNm

Step 7: Trial section

The trial section is determined from the design of uniaxial bending with P

u

= 1700 kN and M

u

=

22

1.15( )

ux uy

MM

. So, we have = (1.15){(103.6)

2

+ (95.13)

2

}

1/2

= 161.75 kNm. With

these values of P

u

(= 1700 kN) and M

u

(= 161.75 kNm), we use chart of SP-16 for the Dd

0.134. We assume the diameters of longitudinal bar as 25 mm, diameter of lateral tie = 8 mm

and cover = 40 mm, to get = 40 + 8 + 12.5 = 60.5 mm. Accordingly,

/dD



= 60.5/450 =

0.134 and

/db



= 60.5/350 = 0.173.

P

u

/f

ck

bD = 1700(10

3

)/(30)(350)(450) = 0.3598

M

u

/f

ck

bD

2

= 161.75(10

6

)/(30)(350)(450)(450) = 0.076

We have to interpolate the values of p/f

ck

for

/dD



= 0.134 obtained from Charts 44 (for

/dD



= 0.1) and 45 (

/dD



= 0.15). The values of p/f

ck

are 0.05 and 0.06 from Charts 44 and

45, respectively. The corresponding values of p are 1.5 and 1.8 per cent, respectively. The

interpolated value of p for = 0.134 is 1.704 per cent, which gives A

sc

= (1.704)(350)(450)/100

= 2683.8 mm

2

. We use 4-25 + 4-20 (1963 + 1256 = 3219 mm

2

), to have p provided = 2.044

per cent giving p/f

ck

= 0.068.

Step 8: Calculation of balanced loads P

b

The values of P

bx

and P

by

are determined using Table 60 of SP-16. For this purpose, two

parameters k

1

and k

2

are to be determined first from the table. We have p/f

ck

= 0.068,

/dD



=

0.134 and

/db



= 0.173. From Table 60, k

1

= 0.19952 and k

2

= 0.243 (interpolated for

/dD



= 0.134) for P

bx

. So, we have: P

bx

/f

ck

bD = k

1

+ k

2

(p/f

ck

) = 0.19952 + 0.243(0.068) = 0.216044,

which gives P

bx

= 0.216044(30)(350)(450)(10

-3

) = 1020.81 kN.

Similarly, for P

by

:

/dD



= 0.173, p/f

ck

= 0.068. From Table 60 of SP-16, k

1

= 0.19048 and k

2

= 0.1225 (interpolated for

/db



= 0.173). This gives P

by

/f

ck

bD = 0.19048 + 0.1225(0.068) =

0.19881, which gives P

by

= (0.19881)(30)(350)(450)(10

-3

) = 939.38 kN.

Since, the values of P

bx

and P

by

are less than P

u

, the modification factors are to be used.

Step 9: Determination of P

uz

Method 1: From Eq.10.59 of Lesson 26

P

uz

= 0.45 f

ck

A

g

+ (0.75 f

y

 0.45 f

ck

) A

sc

= 0.45(30)(350)(450) + {0.75(415)  0.45(30)}(3219) = 3084.71 kN

Step 10: Determination of modification factors

k

ax

= (P

uz

– P

u

)/(P

uz

– P

ubx

)

or k

ax

= (3084.71  1700)/(3084.71  1020.81) = 0.671 and

k

ay

= (P

uz

– P

u

)/(P

uz

– P

uby

)

or k

ay

= (3084.71  1700)/(3084.71  939.39) = 0.645

The values of the two modification factors are different from the assumed value of 0.55 in

Step 5. However, the moments are changed and the section is checked for safety.

Step 11: Total moments incorporating modification factors

M

ux

= M

ox

(from Step 4) + (k

ax

) M

ax

(from Step 3)

= 52.7 + 0.671(92.548) = 114.8 kNm

M

uy

= M

oy

(from Step 4) + k

ay

(M

ay

) (from Step 3)

= 47.04 + (0.645)(87.43) = 103.43 kNm.

Step 12: Uniaxial moment capacities

The two uniaxial moment capacities M

ux1

and M

uy1

are determined as stated: (i) For M

ux1

, by

interpolating the values obtained from Charts 44 and 45, knowing the values of P

u

/f

ck

bD =

0.3598 (see Step 7), p/f

ck

= 0.068 (see Step 7),

/dD



= 0.134 (see Step 7), (ii) for M

uy1

, by

interpolating the values obtained from Charts 45 and 46, knowing the same values of P

u

/f

ck

bD

and p/f

ck

as those of (i) and

/dD



= 0.173 (see Step 7). The results are given below:

(i) M

ux1

/f

ck

bD

2

= 0.0882 (interpolated between 0.095 and 0.085)

(ii) M

uy1

/f

ck

bb

2

= 0.0827 (interpolated between 0.085 and 0.08)

So, we have, M

ux1

= 187.54 kNm and M

uy1

= 136.76 kNm.

Step 13: Value of

n



We have P

u

/P

uz

= 1700/3084.71 = 0.5511. We have

n



= 0.67 + 1.67 (P

u

/P

uz

) = 1.59.

Step 14: Checking of column for safety

11

( / ) ( / ) 1

nn

ux ux uy uy

M M M M





Here, putting the values of M

ux

, M

ux1

, M

uy

, M

uy1

and n   

1.5452

+

(103.43/136.76)

1.5852

= 0.4593 + 0.6422 = 1.1015. Hence, the section or the reinforcement has

to be revised.

Step R9: Determination of P

uz

P

uz

= 0.45(30)(350)(450) + {0.75(415)  0.45(30)}(3927) = 3295.514 kN.

Step R10: Determination of modification factors

k

ax

= (3295.514  1700)/(3295.514  1038.145) = 0.707

k

ay

= (3295.514  1700)/(3295.514  948.12) = 0.68

Step R11: Total moments incorporating modification factors

M

ux

= 52.70 + 0.707(92.548) = 118.13 kNm

M

uy

= 47.04 + 0.68(87.43) = 106.49 kNm

Step R12: Uniaxial moment capacities

Using Charts 44 and 45 for M

ux1

and Charts 45 and 46 for M

uy1

, we get (i) the coefficient

0.1032 (interpolating 0.11 and 0.10) and (ii) the coefficient 0.0954 (interpolating 0.1 and

0.09) for M

ux1

and M

uy1

, respectively.

M

ux1

= (0.1032)(30)(350)(450)(450)(10

-6

) = 219.429 kNm

M

uy1

= (0.0954)(30)(450)(350)(350)(10

-6

) = 157.77 kNm

Step R13: Value of

n



P

u

/P

uz

= 1700/3295.514 = 0.5158 which gives

n = 1 + (0.5158  0.2)/0.6 = 1.5263

Step R14: Checking of column for safety

(118.13/219.424)

1.5263

+ (106.49/157.77)

1.5263

= 0.3886 + 0.5488 = 0.9374 < 1.0

Hence, the revised reinforcement is safe.

Design of isolated column footing.

The superstructure is placed on the top of the foundation structure, designated as substructure as

they are placed below the ground level. The elements of the superstructure transfer the loads and

moments to its adjacent element below it and finally all loads and moments come to the

foundation structure, which in turn, transfers them to the underlying soil or rock. Thus, the

foundation structure effectively supports the superstructure. However, all types of soil get

compressed significantly and cause the structure to settle. Accordingly, the major requirements of

the design of foundation structures are the two as given below (see cl.34.1 of IS 456):

1. Foundation structures should be able to sustain the applied loads, moments, forces and

induced reactions without exceeding the safe bearing capacity of the soil.

2. The settlement of the structure should be as uniform as possible and it should be within the

tolerable limits. It is well known from the structural analysis that differential settlement of

supports causes additional moments in statically indeterminate structures. Therefore,

avoiding the differential settlement is considered as more important than maintaining uniform

overall settlement of the structure.

Types of Foundation Structures

1. Shallow Foundation

Shallow foundations are used when the soil has sufficient strength within a short depth below the

ground level. They need sufficient plan area to transfer the heavy loads to the base soil. These

heavy loads are sustained by the reinforced concrete columns or walls (either of bricks or

reinforced concrete) of much less areas of cross-section due to high strength of bricks or

reinforced concrete when compared to that of soil. The strength of the soil, expressed as the safe

bearing capacity of the soil is normally supplied by the geotechnical experts to the structural

engineer. Shallow foundations are also designated as footings. The different types of shallow

foundations or footings are discussed below.

(i) Plain concrete pedestal footings

(ii) Isolated footings

(iii) Combined footings

(iv) Strap footings

(v) Strip foundation or wall footings

(vi) Raft or mat foundation

2. Deep foundations

As mentioned earlier, the shallow foundations need more plan areas due to the low strength

of soil compared to that of masonry or reinforced concrete. However, shallow foundations are

selected when the soil has moderately good strength, except the raft foundation which is good

in poor condition of soil also. Raft foundations are under the category of shallow foundation

as they have comparatively shallow depth than that of deep foundation. It is worth

mentioning that the depth of raft foundation is much larger than those of other types of

shallow foundations.

However, for poor condition of soil near to the surface, the bearing capacity is very less and

foundation needed in such situation is the pile foundation. Piles are, in fact, small diameter

columns which are driven or cast into the ground by suitable means. Precast piles are driven

and cast-in-situ are cast. These piles support the structure by the skin friction between the pile

surface and the surrounding soil and end bearing force, if such resistance is available to

provide the bearing force. Accordingly, they are designated as frictional and end bearing

piles. They are normally provided in a group with a pile cap at the top through which the

loads of the superstructure are transferred to the piles.

Piles are very useful in marshy land where other types of foundation are impossible to

construct. The length of the pile which is driven into the ground depends on the availability

of hard soil/rock or the actual load test. Another advantage of the pile foundations is that they

can resist uplift also in the same manner as they take the compression forces just by the skin

friction in the opposite direction.

However, driving of pile is not an easy job and needs equipment and specially trained persons

or agencies. Moreover, one has to select pile foundation in such a situation where the

adjacent buildings are not likely to be damaged due to the driving of piles. The choice of

driven or bored piles, in this regard, is critical.

Exhaustive designs of all types of foundations mentioned above are beyond the scope of this

course. Accordingly, this module is restricted to the design of some of the shallow footings,

frequently used for normal low rise buildings only.

Isolated Footing

Figure 3.8: Uniform and rectangular footing

Design Considerations

(a) Minimum nominal cover (cl. 26.4.2.2 of IS 456)

The minimum nominal cover for the footings should be more than that of other structural

elements of the superstructure as the footings are in direct contact with the soil. Clause

26.4.2.2 of IS 456 prescribes a minimum cover of 50 mm for footings. However, the actual

cover may be even more depending on the presence of harmful chemicals or minerals, water

table etc.

(b) Thickness at the edge of footings (cls. 34.1.2 and 34.1.3 of IS 456)

The minimum thickness at the edge of reinforced and plain concrete footings shall be at least

150 mm for footings on soils and at least 300 mm above the top of piles for footings on piles,

as per the stipulation in cl.34.1.2 of IS 456.

rough

the bottom edge of the pedestal and the corresponding junction edge of the column with

pedestal and the horizontal plane shall be determined from the following expression

(cl.34.1.3 of IS 456)

0.5

tan 0.9{(100 / ) 1}

a ck

qf





where q

a

= calculated maximum bearing pressure at the base of pedestal in N/mm

2

, and

f

ck

= characteristic strength of concrete at 28 days in N/mm

2

.

(c) Bending moments (cl. 34.2 of IS 456)

1. It may be necessary to compute the bending moment at several sections of the footing

depending on the type of footing, nature of loads and the distribution of pressure at the base

of the footing. However, bending moment at any section shall be determined taking all forces

acting over the entire area on one side of the section of the footing, which is obtained by

passing a vertical plane at that section extending across the footing (cl.34.2.3.1 of IS 456).

2. The critical section of maximum bending moment for the purpose of designing an isolated

concrete footing which supports a column, pedestal or wall shall be:

(i) at the face of the column, pedestal or wall for footing supporting a concrete column,

pedestal or reinforced concrete wall, and

(ii) halfway between the centre-line and the edge of the wall, for footing under masonry wall.

This is stipulated in cl.34.2.3.2 of IS 456.

The maximum moment at the critical section shall be determined as mentioned in 1 above.

For round or octagonal concrete column or pedestal, the face of the column or pedestal shall

be taken as the side of a square inscribed within the perimeter of the round or octagonal

column or pedestal (see cl.34.2.2 of IS 456 and Figs.11.28.13a and b).

(d) Shear force (cl. 31.6 and 34.2.4 of IS 456)

Footing slabs shall be checked in one-way or two-way shears depending on the nature of

bending. If the slab bends primarily in one-way, the footing slab shall be checked in one-way

vertical shear. On the other hand, when the bending is primarily two-way, the footing slab

shall be checked in two-way shear or punching shear. The respective critical sections and

design shear strengths are given below:

1. One-way shear (cl. 34.2.4 of IS 456)

One-way shear has to be checked across the full width of the base slab on a vertical section

located from the face of the column, pedestal or wall at a distance equal to

(i) effective depth of the footing slab in case of footing slab on soil, and

(ii) half the effective depth of the footing slab if the footing slab is on piles.

The design shear strength of concrete without shear reinforcement is given in Table 19 of

cl.40.2 of IS 456.

2. Two-way or punching shear (cls.31.6 and 34.2.4)

Two-way or punching shear shall be checked around the column on a perimeter half the

effective depth of the footing slab away from the face of the column or pedestal.

The permissible shear stress, when shear reinforcement is not provided, shall not exceed

sc

k



, where k

s

= (0.5 + ccg the ratio of short side to long side of

the column, and

c



= 0.25(f

ck

)

1/2

in limit state method of design, as stipulated in cl.31.6.3 of

IS 456.

Normally, the thickness of the base slab is governed by shear. Hence, the necessary thickness

of the slab has to be provided to avoid shear reinforcement.

(e) Bond (cl.34.2.4.3 of IS 456)

The critical section for checking the development length in a footing slab shall be the same

planes as those of bending moments in part (c) of this section. Moreover, development length

shall be checked at all other sections where they change abruptly. The critical sections for

checking the development length are given in cl.34.2.4.3 of IS 456, which further

recommends to check the anchorage requirements if the reinforcement is curtailed, which

shall be done in accordance with cl.26.2.3 of IS 456.

(f) Tensile reinforcement (cl.34.3 of IS 456)

The distribution of the total tensile reinforcement, calculated in accordance with the moment

at critical sections, as specified in part (c) of this section, shall be done as given below for

one-way and two-way footing slabs separately.

(i) In one-way reinforced footing slabs like wall footings, the reinforcement shall be

distributed uniformly across the full width of the footing i.e., perpendicular to the direction of

wall. Nominal distribution reinforcement shall be provided as per cl. 34.5 of IS 456 along the

length of the wall to take care of the secondary moment, differential settlement, shrinkage

and temperature effects.

(ii) In two-way reinforced square footing slabs, the reinforcement extending in each direction

shall be distributed uniformly across the full width/length of the footing.

(iii) In two-way reinforced rectangular footing slabs, the reinforcement in the long direction shall

be distributed uniformly across the full width of the footing slab. In the short direction, a central

band equal to the width of the footing shall be marked along the length of the footing, where the

portion of the reinforcement shall be determined as given in the equation below. This portion of

the reinforcement shall be distributed across the central band:

Figure 3.10 Bands for reinforcement in rectangular footing



Where 3.10).

Each of the two end bands shall be provided with half of the remaining reinforcement, distributed

uniformly across the respective end band.

(g) Transfer of load at the base of column (cl.34.4 of IS 456)

All forces and moments acting at the base of the column must be transferred to the pedestal,

if any, and then from the base of the pedestal to the footing, (or directly from the base of the

column to the footing if there is no pedestal) by compression in concrete and steel and tension

in steel. Compression forces are transferred through direct bearing while tension forces are

transferred through developed reinforcement. The permissible bearing stresses on full area of

concrete shall be taken as given below from cl.34.4 of IS 456:

br



= 0.25f

ck

, in working stress method, and

br



= 0.45f

ck

, in limit state method

The stress of concrete is taken as 0.45f

ck

while designing the column. Since the area of

footing is much larger, this bearing stress of concrete in column may be increased

considering the dispersion of the concentrated load of column to footing. Accordingly, the

permissible bearing stress of concrete in footing is given by (cl.34.4 of IS 456):

br



= 0.45f

ck

(A

1

/A

2

)

1/2

with a condition that

(A

1

/A

2

)

1/2

2

where A

1

= maximum supporting area of footing for bearing which is geometrically similar to

and concentric with the loaded area A

2

.

A

2

= loaded area at the base of the column.

The above clause further stipulates that in sloped or stepped footings, A

1

may be taken as the

area of the lower base of the largest frustum of a pyramid or cone contained wholly within

the footing and having for its upper base, the area actually loaded and having side slope of

one vertical to two horizontal.

If the permissible bearing stress on concrete in column or in footing is exceeded,

reinforcement shall be provided for developing the excess force (cl.34.4.1 of IS 456), either

by extending the longitudinal bars of columns into the footing (cl.34.4.2 of IS 456) or by

providing dowels as stipulated in cl.34.4.3 of IS 456 and given below:

(i) Sufficient development length of the reinforcement shall be provided to transfer the

compression or tension to the supporting member in accordance with cl.26.2 of IS 456, when

transfer of force is accomplished by reinforcement of column (cl.34.4.2 of IS 456).

(ii) Minimum area of extended longitudinal bars or dowels shall be 0.5 per cent of the cross-

sectional area of the supported column or pedestal (cl.34.4.3 of IS 456).

(iii) A minimum of four bars shall be provided (cl.34.4.3 of IS 456).

(iv) The diameter of dowels shall not exceed the diameter of column bars by more than 3

mm.

(v) Column bars of diameter larger than 36 mm, in compression only can be doweled at the

footings with bars of smaller size of the necessary area. The dowel shall extend into the

column, a distance equal to the development length of the column bar and into the footing, a

distance equal to the development length of the dowel, as stipulated in cl.34.4.4 of IS 456.

(h) Nominal reinforcement (cl. 34.5 of IS 456)

Clause 34.5.1 of IS 456 stipulates the minimum reinforcement and spacing of the bars in

footing slabs as per the requirements of solid slab (cls.26.5.2.1 and 26.3.3b(2) of IS 456,

respectively).

Numerical Problem

Design an isolated footing of uniform thickness of a RC column bearing a vertical load of

600 KN and having a base of size 500x500 mm. the safe bearing capacity of soil may be

taken as 120 KN/m2. Use M20 concrete and Fe 415 steel.

Solution

Size of footing

W=600 KN;

Self weight of footing @ 10% =60 KN

Total load =660 KN

Size of footing = 660/120 = 5.5 m

2

Since square footing , B=

5.5

=2.345 m2

Provide a square footing = 2.4mx 2.4m

Net upward pressure , p

0

= 600/(2.4x2.4) = 104.17 KN/m

2

Design of section

The maximum BM acts at the face of column

M=

2

( ) 112.8

8

o

B

p B b KN m  

Mu = 1.5M =169.2 KN-m

Therefore d = 160 mm; D = 160+60 = 220mm

Depth on the basis of one-way shear



where shear force V is given by

{0.5( ) } 104.17 2.4{0.5 (2.4 0.5) 0.001 }

o

V p B B b d x x d     

Vu = 1.5V

375012(0.95 0.001 )

2400

u

c

V

d

bd d







From table B.5.2.1.1 of IS 456:2000 k=1.16 for D = 220mm.

Also for under-reinforced section with p

t

= 0.3% for M20 concrete,

c



=0.384 N/mm

2

.

Hence design shear stress = k

c



=0.445 N/mm

2

From which we get d= 246.7 250 mm

Depth for two way shear

Take d greater one of the two i.e. 250mm. for two-way shear, the section lies at d/2 from the

column face all round. The width bo of the section = b+d = 750mm

Shear force around the section

22

[ ] 541.42

oo

F p B b KN  

Fu=1.5F

6

2

812.13 10

1.083 /

4 4 750 250

u

v

o

F

x

N mm

b d x x



  

Permissible shear stress =

sc

k



Where

(0.5 ) (0.5 1)

sc

k



   

with a maximum value 1. ks=1

0.25

c ck

f





=1.118 N/mm2

Permissible shear stress= 1.118 N/mm2

Hence safe.

Hence d=250 mm, using 60 mm as effective cover and keeping D=330 mm, effective depth =

330-60= 270 mm in one direction and other direction d=270- 12 =258 mm.

Calculation of reinforcement

A

st

= 1944 mm

2

Using 12 mm bars, spacing required = 138.27 mm

So provide 12 mm @ 125 c/c in each direction.

Development length

L

d

=564 mm

Provide 60 mm side cover, length of bars available =0.5[B-b]-60=890 mm >L

d

So safe.

Transfer of load at column base

A2= 500x500 = 250000 mm

2

A1=[500+2(2x330)]= 3312400 mm

2

1

2

3.64

A



Taking

1

2

A

=2

Hence permissible bearing stress = 18 KN/m

2

Actual bearing stress = 3.6 N/mm

2

Hence safe.

MODULE-4

Introduction

Masonry is one of the main items of construction in a building and needs careful

consideration. It comprises masonry units such as brick, stone, concrete block laid in mortar.

There is a large variety of units and a number of different types and grades of mortars that are

used in masonry. Architects and Engineers should have good knowledge of properties of

units and mortars so as to be able to choose an appropriate combination of the two, to meet

the requirements for a particular situation.

STRUCTURAL DESIGN

General

i) Some general guidance on the design concept of load bearing masonry structures is given

in the following paragraphs.

ii) A building is basically subjected to two types of loads, namely:

a) Vertical loads on account of dead loads of materials used in construction, plus live loads

due to occupancy; and

b) Lateral loads due to wind and seismic forces. While all walls in general can take vertical

loads, ability of a wall to take lateral loads depends on its disposition in relation to the

direction of lateral load. This could be best explained with the help of an illustration. In Fig.

4.1, the wall A has good resistance against a lateral load, while wall B offers very little

resistance to such load. The lateral loads acting on the face of a building are transmitted

through floors (which act as horizontal beams) to cross walls which act as horizontal beams)

to cross walls which act as shear walls. From cross walls, loads are transmitted to the

foundation. This action is illustrated in Fig. 4.2. Stress pattern in cross walls due to lateral

loads is illustrated in Fig. 4.3.

FIG. 4.1 ABILITY OF A WALL TO TAKE LATERAL LOADS

FIG. 4.2 Function of Lateral Support to Wall

FIG. 4.3 Stress Pattern in Cross Wall Acting as Shear Wall

iii) As a result of lateral load, in the cross walls there will be an increase of compressive

stress on the leeward side, and decrease of compressive stress on the windward side. These

w 

interest to note that a wall which is carrying-greater vertical loads, will be in a better position

to resist lateral loads than the one which is lightly loaded in the vertical direction. This point

should be kept in view while planning the structure so as to achieve economy in structural

design.

iv) A structure should have adequate stability in the direction of both the principal axes. The

truction may not have much lateral resistance in the longitudinal

direction. In multi-          

construction from consideration of stability and economy as illustrated in Fig. E-19.

Fig. 4.4 Stability Of Cross Wall and Cellular (Box Type) Construction

v) Size, shape and location of openings in the external walls have considerable influence on

stability and magnitude of stresses due to lateral loads. vi) If openings in longitudinal walls

are so located that portions of these walls act as flanges to cross walls, the strength of the

cross walls get considerably increased and structure becomes much more stable.

vii) Ordinarily a load-bearing masonry structure is designed for permissible compressive and

shear stresses (with no tension) as a vertical cantilever by accepted principles of engineering

mechanics. No moment transfer is allowed for, at floor to wall connections and lateral forces

are assumed to be resisted by diaphragm action of floor, roof slabs, which acting as

horizontal beams, transmit lateral forces to cross walls in proportion to their relative stiffness

(moment of inertia).

Numerical Problem

A hall as shown in Fig and of inside dimensions 10.0 m X 20.0 m with a clear height of 5.5 m

up to the bottom of beam is to be constructed with load bearing masonry walls using modular

bricks. Calculate thickness of walls, strength of bricks and grade of mortar for longitudinal

and cross walls, assuming a wind pressure of 1 200 N/m

2

.

Solution:

1) Design Data/ Assumptions

Roof consists of RCC T-beams 40 cm X 80 cm with RCC slab 12 cm thick, beams being at

4.0 m centres. Roof is covered with lime concrete terrace of 15 cm average thickness.

Height of parapet = 20 cm above slab level

Plinth height = 0.5 m

Height of plinth above foundation footing = 0.7 m

2) Minimum thickness of Walls

According to 4.6.1 of the Code, maximum SR = 27, assuming cement or cement-lime mortar

Long wall

H = 0.7 + 5.5 + 0.8/2= 6.6 m

h = 0.75 H = 0.75 X 6.6 = 4.95 m

Slenderness Ratio (SR) = h/t

Therefore t = h/SR = 4.95/27 = 18 cm

In view of long spans and assuming that joints are raked to a depth of 1.0 cm on both sides

adopt 1% brick wall with actual thickness = 29 cm, that is, nominal thickness 30 cm.

Cross wall

H = 0.7 + 5.5 + (0.80 - 0.06)

(from top of footing to centre of slab)

= 6.94 m

h = 0.75 H = 0.75 X 6.94 m

= 5.21 m

t=h/SR=5.21/27 = 19 cm

Adopt 30 cm nominal thickness for cross walls.

3) Loads :

Roof load

RCC slab = 12 X 250 = 3000 N/m2

Terrace = 15 X 200 = 3000 N/m2

Live load = 1500 N/m2

Total = 7 500 N/m2

Self-weight of beam

= 40(80 - 12) X 25 000/(100 x 100)

=6800 N/m

Effective span of beam

= 10 + 0.3

=10.3 m

Load on long walls

Load from beam = (750 X 4 + 680)10.3/ 2

=190000 N=190 kN

Self load of wall including parapet assuming 3 cm plaster thickness. Since we will be

considering combined stresses due to vertical loads and wind load, we will work out all loads

at the top of foundation footing which is

(29 + 3) (0.7 + 5.5 + 0.8 + 0.2) X 20 X 10

3

/100

= 4.61 X 10

4

N/m

Load on cross walls

Slab load = 7500x4/2 = 15000 N/m

= 15 kN/m

Total load on wall at plinth level

= 46.1 + 15 = 61.1 kN/m

4) Stress in Walls Due to Vertical Loads Longwall

2.5 m length of wall will bear weight of 4.0 m length of wall, because of openings.

Stress at footing-top level due to self weight =4.61 X 10

4

X 4.0/(2.5 X 26 X 100)

=28.4 N/cm2 = 0.28 N/mm2

Stress due to concentrated load from beam

Load will spread on

b + 4t = 0.04 + 4 X 0.29

= 1.20 m length of wall

Stress at plinth level due to concentrated load =190000/(1.56 X 26 X 100) = 46 N/cm2= 0.46

N/m2

Therefore total axial at plinth level

= 0.28 + 0.46

= 0.74 N/mm*

Cross wall without opening (Wall a)

61.1 X lo3

Compressive stress = 26 x 103/(26x100) = 23.5 N/cm2 = 0.24 N/mm2

Cross wall with opening (Wall b)

Compressive stress at plinth level =

3

61.1 10 10

(26 100) (10 1.5)

x

x 

= 27.6 N/cm2 = 0.28 N/mm*

5) Stresses Due to Lateral Loads and Combined Stresses

i) Long walls

Since long walls are not adequately stiffened in accordance with the requirements of clause

4.2,2.2(b) of the Code and hall is longer than 8.0 m, it is necessary to work out bending

stresses due to wind load in longitudinal as well as cross wall. Obviously wind load normal to

the long walls will be critical and therefore we will work out bending stresses in long as well

as cross walls on account of wind load normal to the long walls.

Wind load on long wall

Wind load P on long wall per bay

=pA

= 1 200 X 4 X (5.5 + 0.8 + 0.2)

= 31 200 N = 31.2 kN

(Wind load on exposed portion of wall below plinth has been ignored)

Total wind load for the building (5 bays) = 31.20 X 5 = 156 kN

Moments due to wind load on long wall

The walls are laterally supported at the top by RCC beams and slabs. It can be assumed that

this lateral support will be adequate as a horizontal girder to transmit the wind force to the

cross walls. The long wall will thus function as a propped cantilever and the maximum

bending moment will be -P H at bottom support as shown in Fig. below.

Maximum B.M. on long wall per bay = PH/8

= 31 200x (0.7 + 5.5 + 0.8/2)/8

=31200X6.6

= 25 740 N.m

= 25.74 kN.m

We have erred on the safe side by including a small portion of height which is actually not

exposed and thus not subject to any wind force.

Bending stress in long wall

3

2 2 4

6 25.74 10 6

4 0.29 10

M Mx x x

f

Z

bd x x

   

= + 46 N/cm2

= + 0.46 N/mm2

Combined stresses in long wall

=-axial stress + bending stress

= 0.74



0.46 = 1.20 N/mm2 or

0.28 N/ mm2 (both compression)

ii) Cross walls

Wind forces are shared by cross walls in the ratios of their stiffness. Since the cross walls are

identical except for a small door opening in the middle in one wall, for practical purposes it

may be assumed that wind loads are shared equally by the 2 walls.

Total wind load on a cross wall may be assumed to be acting at a plane at mid-height of the

cross wall. Thus total B.M. on one cross wall

=(P/2)x(H/2)

= 1 56 000 X (0.7 + 5.5 + 0.8 + 0.2)/(2x2)

= 280.8 X 10

3

N.m

Moment of inertia of cross wall

A part of the long wall will act as a flange with the cross wall and effective overhanging

length of flange (see 4.2.2.5 of the Code) will be actual length of wall up to window, that is,

1.25 m or 6t that is 6 X 0.20 or H/16 that is,

(0.7 + 5.5 + 0.8 + 0.2)/16

= 0.45 m

whichever is less, that is, 0.45 m. Thus I about neutral axis of the wall

32

0.29 10 2(0.45 0.29) 0.29 5.15

12 12

x x x

x





= 24 + 0.9

= 24.9 m

4

Thus bending stresses at extreme fibres

4

280000 5.29

6.0

24.9 10

My x

f

I

x

     

N/cm2= 0.06 N/mm2

Combined stress in cross walls

= axial stress + bending stress

In case of cross wall ‘a’ combined stresses are

= 0.24 + 0.06 = 0.30 N/mm2 or

0.18 N/ mm2 (both compressive)

ln case of cross wall ‘b’ combined stresses are

= 2.8



0.6 = = 0.34 N/ mm2 or 0.22 N/mm2

(both compressive)

Check for shear stress in cross walls

We will consider wall ‘b’ which will have greater

shear stress

Shear load on the cross wall

= 156 X lo3

= 78.0: lo3 N

Section of wall being rectangular, we will assume parabolic shear distribution and maximum

shear stress will be 1.5 times the average shear. Since flanges do not make any contribution

for resisting shear load, maximum shear stress on wall

=78.00 X 10

3

X 1.5/(0.26x(10-1.5)x10

4

)

= 5.3 N/cm2

= 0.05 N/mm2

Permissible shear stress (see 5.4.3 of the Code), assuming mortar to be of Ml grade.

Fs=0.1+fd/6 where fd is axial compressive stress on the wall due to dead load.

fd = stress due to self load of wall + stress due to dead load from slab

=( 61.1 X 10

3

+ 6 X 10

3

X 2)/(26X 100) = 28 N/cm2= 0.28 N/mm2

Thus

Fs=0.1+0.28/6 =0.14 N/mm2 .

 safe in shear. In fact since actual shear stress is

about one third of permissible shear for Ml mortar, we could use M2 mortar. Thus both cross

walls are safe in tension as well as shear.

6) Masonry for Walls

i) Long walls

Masonry of long walls should be designed for maximum compressive stress that is, 1.19

N/mm

SR=h/t

= 0.75(0.7 + 5.5 + 0.4)/0.26

= 19

Stress reduction factor ks from Table 9 of the code = 0.65

Therefore Basic compressive stress for masonry for unity

Shape modification factor

=- 1.19/0.65

= 1.83 N/mm2

Referring to Table 8 and Table 10, bricks should. be of strength 25 N/mm2 and mortar should

be of grade Hl. If bricks of this strength are not locally available it would be necessary to

introduce piers under the beams so as to increase the supporting area thereby reducing stress

in masonry.

ii) Masonry for cross walls

Masonry of cross wall should be designed for maximum compressive stress that is, 0.34

N/mm2

SR=h/t

= 75 X (0.7 + 5.5 + 0.8 - 0.06)/0.26

=20

Stress reduction factor from Table 9 = 0.62

Basic compressive stress for unity Shape modification factor=- 0.34/0.62 = 0.55 N/mm2

Referring to Tables 8 and 10 of the Code, bricks should be of strength 7.5 N/mm2 and with

Shape modification factor equal to 1 .I.

Thus basic stress of masonry required

0.55/1.1= 0.5 N/mm2

Therefore, Grade .of mortar should be M3. However from the consideration of shear stress,

we should use grade M2 mortar.

Design of columns

Numerical Problem

Design a brick masonry column which carries a super imposed axial compressive load of 100

KN at base of column. Take effective heights of column as 3.0m Design the footing if SBC

of soil is 100 KN/m

2

.

Solution

The super imposed load at the base of column =100 KN

Using H@ grade of mortar (CM=1:2), permissible axial compressive load for a short column

(SR<= 12) from table 8 =0.96 N/mm2

Area of section required = 100x1000/0.96 = 104166 mm2

Provide 345mmx345mm square section of column.

Area provided =119625 mm2

Therefore, SR = 3x1000/345 = 8.695

Therefore it is a short column.

Load on soil assuming 15% as self weight of footing =100x1.15= 115 KN

Net SBC of soil = 115/100 =1.15 m

2

Provide square footing 1.2mx1.2m

Area provide = 1.44 m2 >1.15 m

2