
MBF3C U3L1 Forms of the Quadratic Functions
1
Topic : Forms of Quadratic Functions
Goal : I know the three forms that a quadratic function
can be written in and what information can be
taken directly from the equation for each.
Forms of Quadratic Functions
Using technology, graph each of the following functions.
What do you notice?
A. y = x
2
+ 2x - 3
B. y = (x + 3)(x - 1)
C. y = (x+1)
2
- 4
They all represent the same parabola!
Standard
Form
y = ax
2
+bx+c
Factored
Form
y = a(x - r)(x - s)
Vertex
Form
y = a(x-h)
2
+k
Graph the parabola and state its properties.
Vertex : _____________________________________
Opening : ___________________________________
Axis of symmetry:_____________________________
Max/Min Value :_______________________________
x-intercepts :_________________________________
y-intercepts : _________________________________
Which properties is each form useful in finding?
y = x
2
+ 2x - 3
y = (x + 3)(x - 1)
y = (x+1)
2
- 4
Standard
Form
y = ax
2
+bx+c
Factored
Form
y = a(x - r)(x - s)
Vertex
Form
y = a(x-h)
2
+k

MBF3C U3L1 Forms of the Quadratic Functions
2
Example 1. For y = -3x
2
+ 4x - 7 state...
a) the direction of opening _____________________
b) does it have a max or min? _____________________
c) the y-intercept? _____________________
y = -3x
2
+ 4x - 7
Example 2. a) What are the x-intercepts of f(x) = (x + 6)(x - 4)?
b) Use the x-intercepts to locate the vertex.
c) What is the y-intercept?
Because of symmetry, the vertex will be directly
between the two intercepts. So take the average
of the intercept points and you will find the x-
coordinate of the vertex.
If you know the x-coordinate of the vertex, the y-
coordinate is simply the value of the function at
that location, so determine f(-1).
y = (x + 6)(x - 4)
NOTE
NOTE
The vertex really is the most important part of the parabola.
Once you know it, you also know
* axis of symmetry * max/min value * range
Practice Questions - Handout Page
When the parabola goes across the y-axis,
the x-value is ZERO. To find the y-intercept,
let x=0.

MBF3C&U3L1&Forms&of&Quadratic&Functions&
!
"#!! $%&!'())(*+,-!&./01+(,2!03&!+,!4$567587!9:8;#!!<=&,1+'>!1%&!?0)/&2!('!0@!A!0,=!B!'(3!&0B%#!
!
! 0C!
€
y = 2x
2
+ 4 x + 8
! 0DEEEEEEEEEEE! ADEEEEEEEEEEEE! BDEEEEEEEEEEEEE!
! AC!
€
y = x
2
+ 9x − 6
! 0DEEEEEEEEEEE! ADEEEEEEEEEEEE! BDEEEEEEEEEEEEE!
! BC!
€
y = −x
2
− 2x
! ! 0DEEEEEEEEEEE! ADEEEEEEEEEEEE! BDEEEEEEEEEEEEE!
! =C!
€
y =
1
2
x
2
−16
!! 0DEEEEEEEEEEE! ADEEEEEEEEEEEE! BDEEEEEEEEEEEEE!
!
F#!! $%&!'())(*+,-!03&!1%&!20G&!&./01+(,2!'3(G!./&21+(,!H"#!!I+3B)&!1%&!0JJ3(J3+01&!3&2J(,2&!(3!
'+))!+,!1%&!A)0,K#!
!
! 0C!
€
y = 2x
2
+ 4 x + 8
! :J&,2!L!M!(3!7! ;0N!(3!;+,! ! >O+,1!L!EEEEEEEEEEEEE!
! AC!
€
y = x
2
+ 9x − 6
! :J&,2!L!M!(3!7! ;0N!(3!;+,! ! >O+,1!L!EEEEEEEEEEEEE!
! BC!
€
y = −x
2
− 2x
! ! :J&,2!L!M!(3!7! ;0N!(3!;+,! ! >O+,1!L!EEEEEEEEEEEEE!
! =C!
€
y =
1
2
x
2
−16
!! :J&,2!L!M!(3!7! ;0N!(3!;+,! ! >O+,1!L!EEEEEEEEEEEEE!
!
P#!! $%&!'())(*+,-!./0=301+B!&./01+(,2!03&!+,!95I$:8Q7!9:8;#!!9+))!+,!1%&!'())(*+,-!B%031#!!R(/!
*+))!,&&=!1(!=(!2(G&!*(3K!(,!0!2B30J!J+&B&!('!J0J&3S!
!
!
!"#$%&"'()
'*)
+,$("(-)
./"(&$#%$,&0)
1''#2"(3&$0)
'*)&4$)5$#&$.)
63.76"()5389$)
:/"(&$#%$,&)
0C!
€
y = (x − 3)(x − 7)
!
!
!
!
T!!!!!!@!!!!!C!
;0N!!!;+,!!
!
AC!
€
y = −(x +1)(x + 9)
!
!
!
!
T!!!!!!@!!!!!C!
;0N!!!;+,!
!
BC!
€
y = −2(x − 4)(x + 2)
!
!
!
!
T!!!!!!@!!!!!C!
;0N!!!;+,!
!
=C!
€
y =
1
2
x(x + 6)
!
!
!
!
T!!!!!!@!!!!!C!
;0N!!!;+,!
!
!
!
U#!! M2&!>(/3!+,'(3G01+(,!'3(G!HP!1(!-30J%!1%&!5V:WQ!&./01+(,2!(,!1%&!-3+=2!A&)(*#!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!

X#!!$%&!'())(*+,-!'/,B1+(,2!03&!+,!WQ8$QY!9:8;#!! 9+) )!+,!1%&!B%031!!
!
3)
4)
;)
<$#&$.)
=."0)'*)
>:??$&#:)
63."?9?)'#)
6"("?9?)<389$)
:/"(&$#%$,&)
0C!!
€
y = (x − 3)
2
+ 2
!
!
!
!
!
!
!
!
AC!
€
y = (x + 4)
2
− 5
!
!
!
!
!
!
!
!
BC!
€
y = −3(x + 1)
2
− 6
!
!
!
!
!
!
!
!
=C!
€
y =
1
2
(x − 2)
2
− 8
!
!
!
!
!
!
!
!
!
Z#!! M2&!>(/3!+,'(3G01+(,!'3(G!HX!1(!-30J%!1%&!5V:WQ!&./01+(,2!(,!1%&!-3+=2!A&)(*#!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
[#!! $%&!-+?&,!-30J%!2%(*2!1%&!%&+-%1O1+G&!3&)01+(,2%+J!('!0!A(11)&!3(BK&1#!
!
!
!
!
!
!
!
!
!
!
!
!
!
! =!
! =C! QN1&,=!1%&!'/,B1+(,!A0BK*03=2!+,1(!,&-01+?&!1+G&#!!\%01!+2!1%&!(1%&3!NO+,1&3B&J1]!
&C!! M2&!1%&!NO+,1&3B&J12!1(!'+,=!1%&!?&31&N#!!\%01!+2!1%&!&./01+(,!('!1%&!-30J%!+,!?&31&N!'(3G#!!
'C!! 4/JJ(2&!1%&!)0/,B%+,-!J)01'(3G!*&3&!)(*&3&=#!!^(*!*(/)=!1%+2!&''&B1!1%&!>O+,1&3B&J1@!
1%&!?&31&N@!0,=!1%&!NO+,1&3B&J1!('!1%&!,&*!-30J%!0,=!+12!%0,-O1+G&#!!
!
!
0C!93(G!*%01!%&+-%1!0A(?&!1%&!-3(/,=!*02!1%+2!
A(11)&!3(BK&1!)0/,B%&=]!
!
!
AC!\%01!+2!1%&!0JJ3(N+G01&!G0N+G/G!%&+-%1!
3&0B%&=]!
!
!
BC!Q21+G01&!1%&!_%0,-!1+G&`!('!1%&!3(BK&1#!
!

MBF3C U3L2 Switching into Standard Form
Topic : Switching to Standard Form
Goal : I can expand and simplify expressions and change
quadratic functions into standard form.
Switching to Standard Form
Let's quickly recap how to expand and simplify...
Example 1. Expand and simplify each of the following polynomials.
a) (2x + 5)(3x - 7)
Use Double
Distributive law
(FOIL) to expand
the brackets
First expand and simplify
the brackets, then multiply
the coefficient through.
b) 7(p - 4)(8 - p)
c) (5t - 3)
2
Remember that when a
bracket is squared, that
means we really have two
of the same brackets
multiplied together.
Switching from Factored form to Standard Form
Write y = 4(x + 3)(x + 5) in standard form.
Basically all I'm asking you to do is to expand and simplify the
expression on the right.
y = 4(x + 3)(x + 5)
First expand and simplify
the brackets, then multiply
the coefficient through.

MBF3C U3L2 Switching into Standard Form
Switching from Vertex form to Standard Form
Write y = 4(x - 3)
2
- 7 in standard form.
Basically all I'm asking you to do is to expand and simplify the
expression on the right.
Write the squared bracket
as two brackets multiplied
together
Multiply the coefficient
through the brackets.
Expand the two brackets.
Simplify and be sure it is in
order of descending
powers of x.
Example 2. Put the following parabolas in standard form.
a) y = 4(x - 6)(x + 3) b) y = 2(x-6)
2
- 8

MBF3C U3L2 Switching into Standard Form
Example 3. A word problem.
A study shows that 60,000 students will attend a play in one week if
the ticket price is 40 dollars. For every 2.50 dollars added to the
ticket price, 2000 fewer students will attend the play.
The amount of money the theatre will earn (before expenses) is
called revenue. Revenue = (# tickets sold)(cost per ticket)
a) What is the revenue when the tickets are $40?
b) The Revenue can be written as a function of "n" where n is the
number of times the price increases by $2.50.
R = (60 000 - 2000n)(40 + 2.5n)
Explain how that equation was found
c) Write the equation in standard form. Graph using technology.
What is the maximum revenue and what ticket price will give it?
Practice Questions - Handout Page

MBF3C&U3L2ws&Forms&of&Quadratic&Functions&
!
1.! a)!State!the!x+intercepts!for!each!of!the!following!functions,!and!use!them!to!find!the!vertex.!
! !
a)!
€
y = (x − 3)(x + 8)
!
!
b)!
€
y = (x − 2)(x − 6)
!
c)
€
y = −(x +1)(x − 9)
!
x+int:!__________!and!________!
x+int:!__________!and!________!
x+int:!__________!and!________!
! b)!Expand!and!simplify!each!equation!above!so!that!it!is!in!STANDARD!FORM.!!What!is!the!
y+intercept?!
! ! !
a)!
b)!
c)!
y+int:!__________!
y+int:!__________!
y+int:!__________!
!
! !
! !!c)!Use!the!5!points!you!have!for!each!parabola!to!sketch!a!graph!on!a!separate!piece!of!
graph!paper.!
!
!
2.!! Complete!all!the!same!steps!from!question!#1!for!the!following!parabolas.!
! !
a)!
€
y = 3(x + 2)(x − 5)
!
!
b)!
€
y = −4(x + 2)
2
!
c)
€
y =
1
2
(x + 6)(x − 4)
!
!
3.!! Express!each!quadratic!function!in!standard!form!and!identify!the!y+intercept.!!Sketch!a!
graph!of!the!function.!
a)!
€
y = (x + 2)
2
+ 3
!
!
b)!
€
y = 3(x − 5)
2
+ 8
!
c)
€
y = −4(x + 3)
2
− 9
!
!
4.!! Expand!and!simplify!using!tools!and!methods!of!your!choice.!!
a)!
€
2 (x − 3) + 3(x − 6)
!
!
b)!
€
y = (y + 4)(y − 4) − (y − 3)(y − 4)
!
c)
€
3( p −1)
2
− 2(p + 3)( p − 4)
!

MBF3C U3L3 Factoring Simple Trinomials
Factoring Simple Trinomials
Topic : Factoring Simple Trinomials
Goal : I know how to factor simple trinomials so that I can
find the x-intercepts of quadratic functions (parabolas)
We saw that when we have a function in factored form, we can easily
pick out the x-intercepts.
So if we want the x-intercepts, it would be nice if we could put the
equation into factored form. In this lesson we discuss how to put a
polynomial into factored form.
We will start by expanding and looking for patterns. We can put all
expansion questions into two categories...
(x+2)(x+5) =
Brackets have the same signs...
Brackets have different signs...
(x-2)(x-5) =
1) Has a constant term that is
always ____________.
(x+2)(x-5) =
(x-2)(x+5) =
So if the brackets have the same
signs, we notice that in the
trinomial answer...
2) Has a middle term that has
the same sign as
1) Has a constant term that is
always ____________.
So if the brackets have different
signs, we notice that in the
trinomial answer...
2) Has a middle term that has
the same sign as

MBF3C U3L3 Factoring Simple Trinomials
Let's use these patterns to write the two brackets that these trinomial
answers come from...
Steps to factoring.
Step 1. Put down two sets of
brackets and place an x at
the front of each.
Step 2. Look at the sign of the constant term.
Step 3. If the constant term is +
Step 3. If the constant term is -
The brackets have the
same sign and it will
be the same as the
sign of the middle
term. So put that sign
in both brackets.
Step 4. Since the constant term
is + we are looking for
two numbers that
multiply to the constant
term and + to the middle
term.
Step 4. Since the constant term
is - we are looking for
two numbers that
multiply to the constant
term and - to the middle
term.
Step 5. Put the bigger of the two
numbers you find in the
bracket with the same
sign as the middle term.
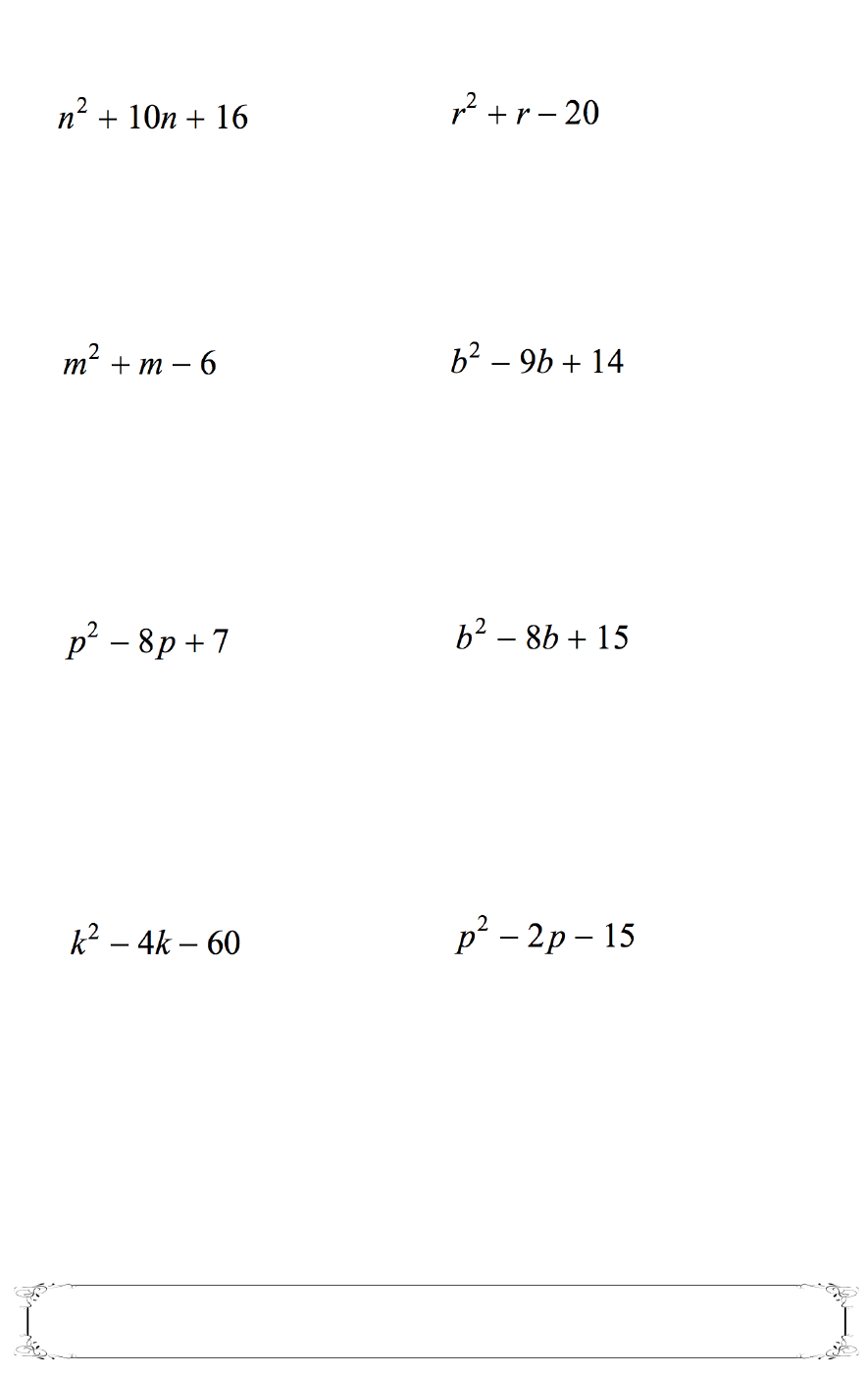
MBF3C U3L3 Factoring Simple Trinomials
More examples. Factor the following...
Practice Questions - Handout Page

MBF3C&U3L3ws&Factoring&Simple&Trinomials&
1.
x
2
+ 9x + 14
2.
x
2
+ 12x + 35
3.
x
2
+ 20x + 36
4.
x
2
+ 15x + 50
5.
x
2
- 20x + 75
6.
x
2
- 33x + 32
7.
x
2
+ 17x + 42
8.
x
2
- 20x + 36
9.
x
2
- 17x + 16
10.
x
2
– 1
11.
x
2
+ 16x + 48
12.
x
2
+ 26x + 48
13.
x
2
+ 15x + 44
14.
x
2
- 10x - 24
15.
x
2
- 18x + 32
16.
x
2
+ 4x - 12
17.
x
2
+ 10x - 24
18.
x
2
-14x -32
19.
x
2
- 4
20.
x
2
+ 28x + 75
21.
x
2
+ 20x + 75
22.
x
2
- 14x + 48
23.
x
2
- 23x + 42
24.
x
2
- 14x + 33
25.
x
2
- x - 12
26.
x
2
- 6x - 16
27.
x
2
- 4x - 32
28.
x
2
- 13x + 36
29.
x
2
– 9
30.
x
2
- 12x + 32
31.
x
2
+ 17x + 70
32.
x
2
-15x - 16
33.
x
2
+10x - 24
34.
x
2
- 16x - 36
35.
x
2
- 6x - 40
36.
x
2
- 10x + 24
37.
x
2
- 8x + 16
38.
x
2
- 5x - 36
39.
x
2
– 25
40.
x
2
- 14x + 24
41.
x
2
- 27x + 50
42.
x
2
- 19x + 48
43.
x
2
- 18x + 45
44.
x
2
+ 15x + 54
45.
x
2
- 5x - 24
46.
x
2
- 16
47.
x
2
- 12x + 32
48.
x
2
- 33x + 32
49.
x
2
– 36
50.
x
2
- 10x + 25
51.
x
2
+ 19x + 60
52.
x
2
- 24x + 44
53.
x
2
- 21x + 54
54.
x
2
+ 11x - 12
55.
x
2
- 23x - 24
56.
x
2
- 10x - 24
57.
x
2
+ 12x + 36
58.
x
2
+ 16x - 36
59.
x
2
– 49
60.
x
2
- 12x + 36
61.
x
2
- 16x + 60
62.
x
2
+ 23x - 24
63.
x
2
+ 4x - 32
64.
x
2
- 3x - 40
65.
x
2
- 13x + 40
66.
x
2
– 64
67.
x
2
+ 13x + 36
68.
x
2
+ 18x + 32
69.
x
2
+ 25x + 24
70.
x
2
- 37x + 36
71.
x
2
+ 14x + 45
72.
x
2
+ 46x + 45
73.
x
2
+ 15x - 16
74.
x
2
+ 6x -16
75.
x
2
- 81
76.
x
2
- 23x + 60
77.
x
2
- 19x + 70
78.
x
2
- 3x - 4
79.
x
2
- 10x - 16
80.
x
2
- 31x - 32
!

MBF3C&U3L3ws&Factoring&Simple&Trinomials&
1.
x
2
+ 9x + 14
2.
x
2
+ 12x + 35
3.
x
2
+ 20x + 36
4.
x
2
+ 15x + 50
5.
x
2
- 20x + 75
6.
x
2
- 33x + 32
7.
x
2
+ 17x + 42
8.
x
2
- 20x + 36
9.
x
2
- 17x + 16
10.
x
2
– 1
11.
x
2
+ 16x + 48
12.
x
2
+ 26x + 48
13.
x
2
+ 15x + 44
14.
x
2
- 10x - 24
15.
x
2
- 18x + 32
16.
x
2
+ 4x - 12
17.
x
2
+ 10x - 24
18.
x
2
-14x -32
19.
x
2
- 4
20.
x
2
+ 28x + 75
21.
x
2
+ 20x + 75
22.
x
2
- 14x + 48
23.
x
2
- 23x + 42
24.
x
2
- 14x + 33
25.
x
2
- x - 12
26.
x
2
- 6x - 16
27.
x
2
- 4x - 32
28.
x
2
- 13x + 36
29.
x
2
– 9
30.
x
2
- 12x + 32
31.
x
2
+ 17x + 70
32.
x
2
-15x - 16
33.
x
2
+10x - 24
34.
x
2
- 16x - 36
35.
x
2
- 6x - 40
36.
x
2
- 10x + 24
37.
x
2
- 8x + 16
38.
x
2
- 5x - 36
39.
x
2
– 25
40.
x
2
- 14x + 24
41.
x
2
- 27x + 50
42.
x
2
- 19x + 48
43.
x
2
- 18x + 45
44.
x
2
+ 15x + 54
45.
x
2
- 5x - 24
46.
x
2
- 16
47.
x
2
- 12x + 32
48.
x
2
- 33x + 32
49.
x
2
– 36
50.
x
2
- 10x + 25
51.
x
2
+ 19x + 60
52.
x
2
- 24x + 44
53.
x
2
- 21x + 54
54.
x
2
+ 11x - 12
55.
x
2
- 23x - 24
56.
x
2
- 10x - 24
57.
x
2
+ 12x + 36
58.
x
2
+ 16x - 36
59.
x
2
– 49
60.
x
2
- 12x + 36
61.
x
2
- 16x + 60
62.
x
2
+ 23x - 24
63.
x
2
+ 4x - 32
64.
x
2
- 3x - 40
65.
x
2
- 13x + 40
66.
x
2
– 64
67.
x
2
+ 13x + 36
68.
x
2
+ 18x + 32
69.
x
2
+ 25x + 24
70.
x
2
- 37x + 36
71.
x
2
+ 14x + 45
72.
x
2
+ 46x + 45
73.
x
2
+ 15x - 16
74.
x
2
+ 6x -16
75.
x
2
- 81
76.
x
2
- 23x + 60
77.
x
2
- 19x + 70
78.
x
2
- 3x - 4
79.
x
2
- 10x - 16
80.
x
2
- 31x - 32
!

MBF3C U3L4 Simple Trinomial Factoring Special Cases
1
Simple Trinomial Factoring - Special Cases
Sometimes a simple trinomial can be disguises as a complex one by a
common factor.
3x
2
+ 3x - 18
At first it looks complicated, but once you realize that you can take out
a common factor of 3, it's really a very simple trinomial to factor.
Special Case #1 - there is a common factor
Topic : Simple Trinomial Factoring - Special Cases
Goal :
I know how to factor some quadratics that have
common factors or are missing terms.
3x
2
+ 3x - 18
So, if you see a number in front of the x
2
-term, you will likely be able
to divide every term in the trinomial by that number. Then you can
just ignore it, and factor as usual.

MBF3C U3L4 Simple Trinomial Factoring Special Cases
2
Special Case #2 - there is no x-term
Special Case #3 - there is no constant term
5x
2
- 45
First of all you want to remove the common factor. The number
in front of x-squared can be divided out of both terms.
Then just know that the middle term missing means that the coefficient
of the x-term must have been zero.
y=4x
2
+20x
First take out the common factor. But this time since the constant
term is missing, you can also divide out an x along with it.
What are the x-
intercepts of this
quadratic function?

MBF3C U3L4 Simple Trinomial Factoring Special Cases
3
Examples. Factor each of the following quadratic expressions.
a) 3x
2
+ 24x + 36
b) 0.5x
2
- 5x + 8
c) 2x
2
- 10x - 48
d) 4x
2
- 100
c) 6x
2
- 30x
Practice Questions - Handout Page

MBF3C U3L5 The Factored Form of a Quadratic Relation
Topic : The Factored Form of a Quadratic Relation
Goal : I know how to graph quadratic equations from the
factored form and how to get information from the
quadratic form of an equation.
The Factored Form of a Quadratic Relation
What kind of things might you need to do with quadratic equations in
factored form? Here are a few examples.
Example 1. Write the following in factored form. What are the x-
intercepts?
b) y = -2(x-1)
2
+8
a) y = x
2
- 4x - 21
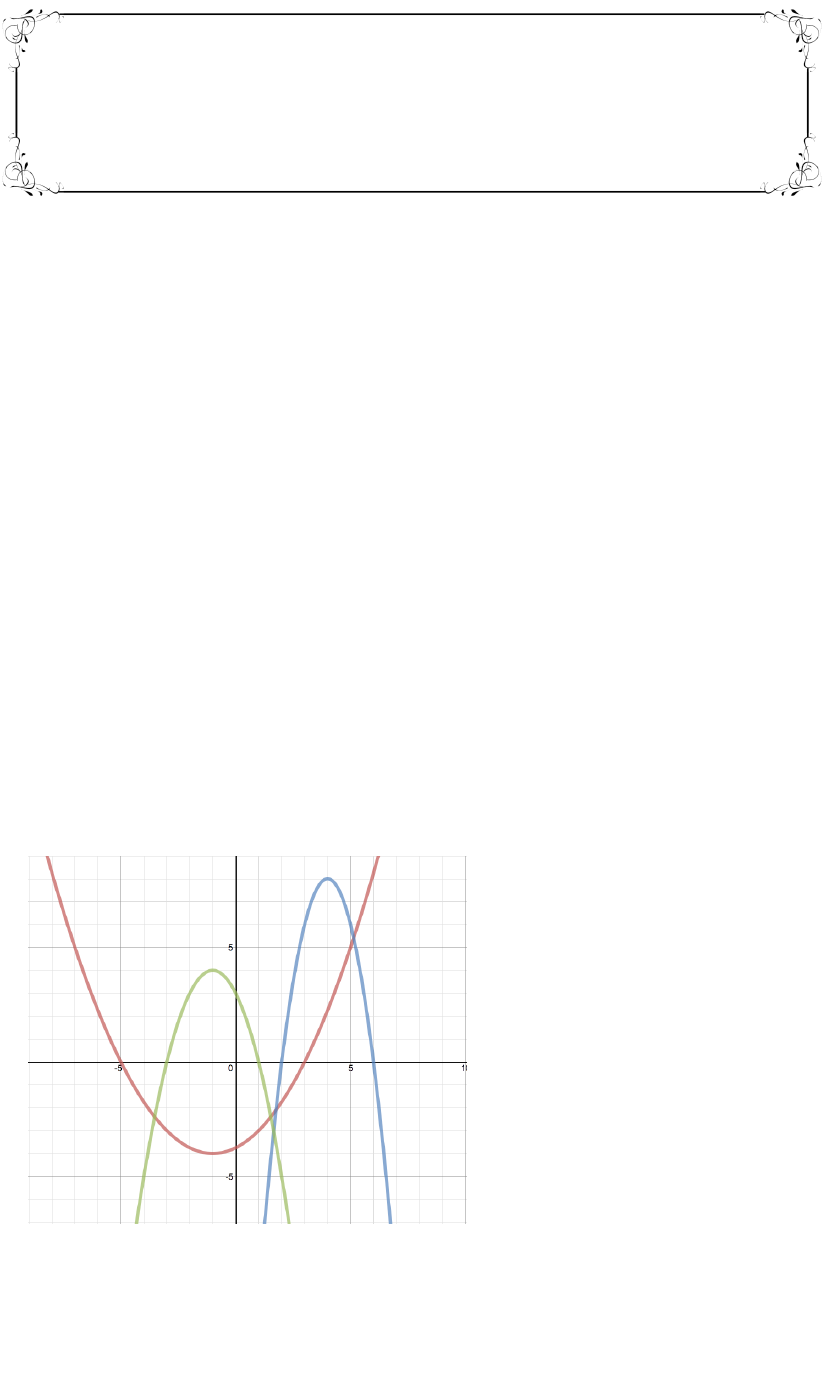
Example 2. Use the graph of the following parabolas to write each
equation in both vertex and factored form.

MBF3C U3L5 The Factored Form of a Quadratic Relation
Example 3. Chose one of the graphs in example two and expand
both equations in standard form. They should both be
the same.
Example 4. Find the vertex of the given equation and graph it on the
grid provided.
Practice Questions - Page 141 #1-6, 9
x-intercepts: _____________
Finding the x-coordinate of the vertex.
Finding the y-coordinate of the vertex.
Now graph using the 3 points you have found - you can find more by
using the a-value and the vertex point.
